Scalar example
Although PROPT is mainly intended to solve for states and control variables that are functions of time, it is possible to use scalar variables as well. (This is often useful when boundary conditions are liked via a system of nonlinear equations.)
This file demonstrates how scalar variables are defined and used in propt.
For a more advanced example, see the Euler buckling problem.
Contents
Equation involving a scalar variable
As an example, consider the equation:
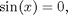
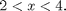
(Note: Even though we only want to solve an equation, we need to set up an entire problem structure, including an independent variable and a cost function. Propt is not really meant to only solve scalar equations.)
% Copyright (c) 2007-2008 by Tomlab Optimization Inc. % Create an "empty" problem problem = proptProblem; problem.name = 'Nonlinear scalar equation'; problem.language = 'Matlab, vectorized'; problem.independent = proptIndependent('t', 0, 1); problem.collocation = proptGausspoints(1); problem.cost = '0'; problem.linobj = 1; % Add a scalar variable, named "x" problem.variables.x = proptScalar(2, 4, 3); % Add an equation, named "eq" problem.equations.eq = proptEquation('sin(x) = 0'); % Solve the problem solution = proptSolve(problem); % Display the result disp(['And the answer is: x = ' num2str(solution.posteval.x)]);
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2009-02-05
=====================================================================================
Problem: --- 1: Nonlinear scalar equation f_k 0.000000000000000000
sum(|constr|) 0.000000000289316693
f(x_k) + sum(|constr|) 0.000000000289316693
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
MAD TB Automatic Differentiation estimating: constraint gradient
FuncEv 1 ConstrEv 3 ConJacEv 3 Iter 2
CPU time: 0.359375 sec. Elapsed time: 0.516000 sec.
And the answer is: x = 3.1416
Optimization involving a scalar variable
Scalar variables can also be used in the objective functions. Example: Maximize
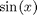
Subject to:
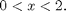
% Create an "empty" problem problem = proptProblem; problem.name = 'Nonlinear scalar equation'; problem.language = 'Matlab, vectorized'; problem.independent = proptIndependent('t', 0, 1); problem.collocation = proptGausspoints(1); % Add a scalar variable, named "x" problem.variables.x = proptScalar(0, 2, 1); % Define the cost function. problem.cost = '-sin(x)'; % Solve the problem solution = proptSolve(problem); % Display the result disp(['And the answer is: x = ' num2str(solution.posteval.x)]);
===== * * * =================================================================== * * * TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2009-02-05 ===================================================================================== Problem: --- 1: Nonlinear scalar equation f_k -1.000000000000000000 Solver: snopt. EXIT=0. INFORM=1. SNOPT 7.2-5 NLP code Optimality conditions satisfied MAD TB Automatic Differentiation estimating: gradient FuncEv 8 GradEv 6 Iter 4 MinorIter 5 CPU time: 0.203125 sec. Elapsed time: 0.235000 sec. And the answer is: x = 1.5708
Optimization/equations involving scalar variables inside phases
There can be an arbitrary number of scalar variables. Variables used at the top level are accessible in any phase, while variables used inside a phase are local to that phase.
% Create an "empty" problem problem = proptProblem; problem.name = 'Nonlinear scalar equation'; problem.language = 'Matlab, vectorized'; problem.variables.y = proptScalar(0, 2, 1); clear v eq t = proptIndependent('t', 0, 1); v.x = proptScalar(0, 2, 1); eq.eq = proptEquation('sin(x*y) = 0.5'); problem.phases.p1 = proptPhase(t, [], v, eq, [], 1); problem.phases.p1.cost = 'x+y'; % We can have a cost inside just one phase. problem.linobj = 1; clear v eq v.x = proptScalar(0, 2, 1); eq.eq = proptEquation('x^2 = y'); problem.phases.p2 = proptPhase(t, [], v, eq, [], 1); % Solve the problem solution = proptSolve(problem); % Display the result disp(['And the answer is: p1: x = ' num2str(solution.posteval.x_p1)]); disp([' p2: x = ' num2str(solution.posteval.x_p2)]); disp([' y = ' num2str(solution.posteval.y)]);
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2009-02-05
=====================================================================================
Problem: --- 1: Nonlinear scalar equation f_k 1.447202427652263000
sum(|constr|) 0.000000078181716323
f(x_k) + sum(|constr|) 1.447202505833979500
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
MAD TB Automatic Differentiation estimating: constraint gradient
FuncEv 1 ConstrEv 8 ConJacEv 8 Iter 5 MinorIter 6
CPU time: 0.218750 sec. Elapsed time: 0.219000 sec.
And the answer is: p1: x = 0.7236
p2: x = 0.85065
y = 0.7236