Batch Fermentor

Dynamic optimization of bioprocesses: efficient and robust numerical strategies 2003, Julio R. Banga, Eva Balsa-Cantro, Carmen G. Moles and Antonio A. Alonso

Case Study I: Optimal Control of a Fed-Batch Fermentor for Penicillin Production

Contents

Problem description

This problem considers a fed-batch reactor for the production of penicillin, as studied by Cuthrell and Biegler (1989). This problem has also been studied by many other authors (Dadebo & McAuley 1995, Banga & Seider 1996, Banga et al. 1997). We consider here the free terminal time version where the objective is to maximize the amount of penicillin using the feed rate as the control variable. It should be noted that the resulting NLP problem (after using CVP) does not seem to be multimodal, but it has been reported that local gradient methods do experience convergence problems if initialized with far-from-optimum profiles, or when a very refined solution is sought. Thus, this example will be excellent in order to illustrate the better robustness and efficiency of the alternative stochastic and hybrid approaches. The mathematical statement of the free terminal time problem is:

Find u(t) and tf over t in [t0; tf ] to maximize

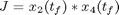
$$ J = x_2(t_f)*x_4(t_f) $$

subject to:

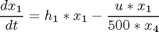
$$ \frac{dx_1}{dt} = h_1*x_1 - \frac{u*x_1}{500*x_4} $$

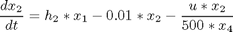
$$ \frac{dx_2}{dt} = h_2*x_1 - 0.01*x_2 - \frac{u*x_2}{500*x_4} $$

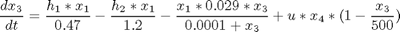
$$ \frac{dx_3}{dt} = \frac{h_1*x_1}{0.47} - \frac{h_2*x_1}{1.2} - \frac{x_1*0.029*x_3}{0.0001+x_3} + u*x_4*(1-\frac{x_3}{500}) $$

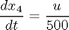
$$ \frac{dx_4}{dt} = \frac{u}{500} $$

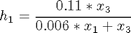
$$ h_1 = \frac{0.11*x_3}{0.006*x_1+x_3} $$

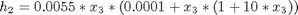
$$ h_2 = 0.0055 * x_3 * (0.0001 + x_3*(1 + 10*x_3)) $$

where x1, x2, and x3 are the biomass, penicillin and substrate concentrations (g=L), and x4 is the volume (L). The initial conditions are:

$$ x(t_0) = [1.5 \ 0 \ 0 \ 7]' $$

There are several path constraints (upper and lower bounds) for state variables (case III of Cuthrell and Biegler, 1989):

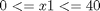
$$ 0 <= x1 <= 40 $$

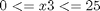
$$ 0 <= x3 <= 25 $$

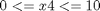
$$ 0 <= x4 <= 10 $$

The upper and lower bounds on the only control variable (feed rate of substrate) are:

$$ 0 <= u <= 50 $$

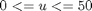
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Solving the problem on multiple grids.

The problem is solved in two stages. First, a solution is computed for a small number of collocation points, then the number of collocation points is increased, and the problem is resolved. This saves time, compared to using the fine grid immediately. 

toms t
toms tfs

% Scale time by factor 100
tf = 100*tfs;

for n=[10 35 70]

    p = tomPhase('p', t, 0, tf, n);
    setPhase(p);

    tomStates x1s x2s x3s x4s
    tomControls us

    % Create scaled states and control
    x1 = 20*x1s;
    x2 = 4*x2s;
    x3 = 0.5*x3s;
    x4 = 10*x4s;
    u  = 10*us;

    % Initial guess
    % Note: The guess for tf must appear in the list before
    % expression involving t.
    if n==10
        x0 = {tf == 126
            icollocate(x1 == 1)
            icollocate(x2 == 1)
            icollocate(x3 == 1)
            icollocate(x4 == 1)
            collocate(u==11.25)};
    else
        % Copy the solution into the starting guess
        x0 = {tf == tf_init
            icollocate(x1 == x1_init)
            icollocate(x2 == x2_init)
            icollocate(x3 == x3_init)
            icollocate(x4 == x4_init)
            collocate(u == u_init)};
    end

    % Box constraints
    % Setting the lower limit for x1 and x4 to slightly more than zero
    % ensures that division by zero is avoided during the optimization
    % process.
    cbox = {tf  <= 256
        1e-8 <= icollocate(x1) <= 40
        0    <= icollocate(x2) <= 50
        0    <= icollocate(x3) <= 25
        1e-8 <= icollocate(x4) <= 10
        0    <= collocate(u)   <= 50};

    % Boundary constraints
    cbnd = initial({x1 == 1.5; x2 == 0
        x3 == 0; x4 == 7});

    % Various constants and expressions
    h1 = 0.11*(x3./(0.006*x1+x3));
    h2 = 0.0055*(x3./(0.0001+x3.*(1+10*x3)));

    % ODEs and path constraints
    ceq = collocate({
        dot(x1) == h1.*x1-u.*(x1./500./x4)
        dot(x2) == h2.*x1-0.01*x2-u.*(x2./500./x4)
        dot(x3) == -h1.*x1/0.47-h2.*x1/1.2-x1.*...
        (0.029*x3./(0.0001+x3))+u./x4.*(1-x3/500)
        dot(x4) == u/500});

    % Objective
    objective = -final(x2)*final(x4);

    % Solution for a small number of collocation points
    options = struct;
    options.name = 'Batch Fermentor';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Batch Fermentor                f_k     -89.207134712354971000
                                       sum(|constr|)      0.000000001143009355
                              f(x_k) + sum(|constr|)    -89.207134711211964000
                                              f(x_0)     -0.000000000000007105

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  150 ConJacEv  150 Iter   90 MinorIter 1388
CPU time: 0.562500 sec. Elapsed time: 0.594000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Batch Fermentor                f_k     -88.164304669313793000
                                       sum(|constr|)      0.000000005721439751
                              f(x_k) + sum(|constr|)    -88.164304663592347000
                                              f(x_0)    -88.778670843009877000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  156 ConJacEv  156 Iter  123 MinorIter  681
CPU time: 1.718750 sec. Elapsed time: 1.719000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Batch Fermentor                f_k     -88.131239012808777000
                                       sum(|constr|)      0.000000000150606711
                              f(x_k) + sum(|constr|)    -88.131239012658170000
                                              f(x_0)    -88.164304669313651000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  314 ConJacEv  314 Iter  252 MinorIter 1231
CPU time: 14.218750 sec. Elapsed time: 14.375000 sec.

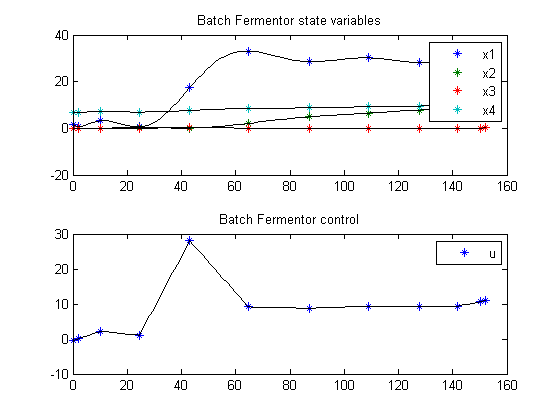
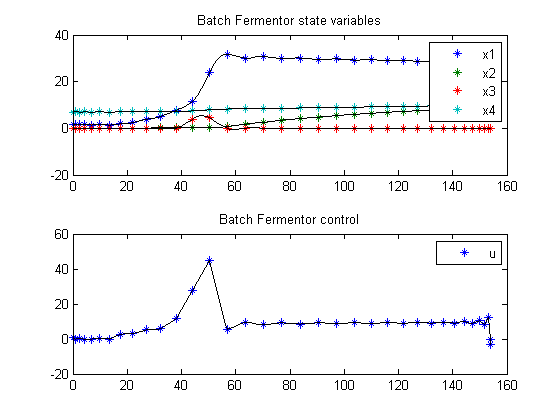
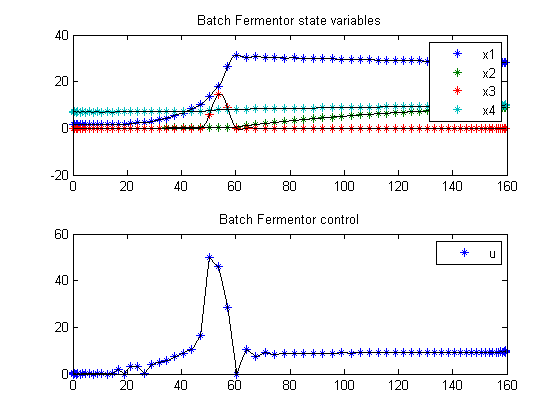
Plot result

    subplot(2,1,1);
    ezplot([x1; x2; x3; x4]);
    legend('x1','x2','x3','x4');
    title('Batch Fermentor state variables');

    subplot(2,1,2);
    ezplot(u);
    legend('u');
    title('Batch Fermentor control');
    drawnow

    % Copy solution for initializing next round
    x1_init  = subs(x1,solution);
    x2_init  = subs(x2,solution);
    x3_init  = subs(x3,solution);
    x4_init  = subs(x4,solution);
    u_init   = subs(u,solution);
    tf_init  = subs(tf,solution);

end