The Brachistochrone Problem

This problem was formulated by Johann Bernoulli, in Acta Eruditorum, June 1696

Contents

Problem description

"Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time."

In this example, we solve the problem numerically for A = (0,0) and B = (10,-3), and an initial speed of zero.

The mechanical system is modelled as follows:

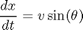
$$ \frac{dx}{dt} = v \sin(\theta) $$

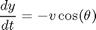
$$ \frac{dy}{dt} = -v \cos(\theta) $$

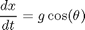
$$ \frac{dx}{dt} = g \cos(\theta) $$

where (x,y) is the coordinates of the point, v is the velocity, and theta is the angle between the direction of movement and the vertical. 

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
toms tf
p = tomPhase('p', t, 0, tf, 20);
setPhase(p);

tomStates x y v
tomControls theta

% Initial guess
% Note: The guess for tf must appear in the list before expression involving t.
x0 = {tf == 10
    icollocate({
    v == t
    x == v*t/2
    y == -1
    })
    collocate(theta==0)};

% Box constraints
cbox = {0.1 <= tf <= 100
    0 <= icollocate(v)
    0 <= collocate(theta) <= pi};

% Boundary constraints
cbnd = {initial({x == 0; y == 0; v == 0})
    final({x == 10; y == -3})};

% ODEs and path constraints
g = 9.81;
ceq = collocate({
    dot(x) == v.*sin(theta)
    dot(y) == -v.*cos(theta)
    dot(v) == g*cos(theta)});

% Objective
objective = tf;

Solve the problem

options = struct;
options.name = 'Brachistochrone';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
x     = subs(collocate(x),solution);
y     = subs(collocate(y),solution);
v     = subs(collocate(v),solution);
theta = subs(collocate(theta),solution);
t =     subs(collocate(t),solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Brachistochrone                f_k       1.878940328102787900
                                       sum(|constr|)      0.000000473296672960
                              f(x_k) + sum(|constr|)      1.878940801399460800
                                              f(x_0)     10.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   45 ConJacEv   45 Iter   30 MinorIter  194
CPU time: 0.125000 sec. Elapsed time: 0.125000 sec.

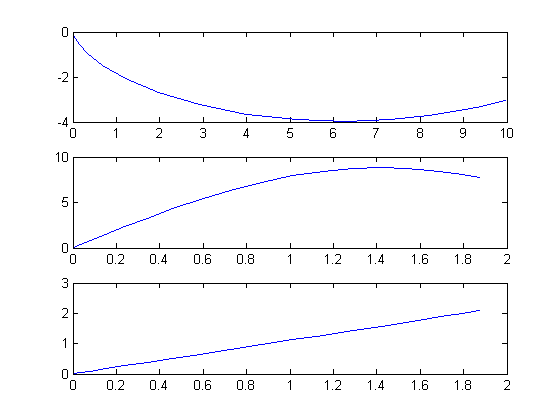
Plot the result

To obtain the brachistochrone curve, we plot y versus x.

subplot(3,1,1)
plot(x, y);

subplot(3,1,2)
plot(t, v);

% We can also plot theta vs. t.
subplot(3,1,3)
plot(t, theta)