Bryson-Denham Two Phase Problem

An example of how the input could look for PROPT.

Contents

Problem description

In this example we also take advantage of the advance knowledge that the solution reaches x1=x1max with x2=0, to introduce an event that divides the time interval into two phases. This increases the accuracy of the solution.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

for n=[5 21]

    toms t1 tcut
    p1 = tomPhase('p1', t1, 0, tcut, n);
    toms t2 tmax
    p2 = tomPhase('p2', t2, tcut, tmax-tcut, n);

    setPhase(p1);
    tomStates x1p1 x2p1
    tomControls up1
    setPhase(p2);
    tomStates x1p2 x2p2
    tomControls up2

    % Constant
    x1max = 1/9;

    setPhase(p1);
    % Initial guess
    if n==5
        x01 = {tcut == 0.25
            tmax == 0.5
            icollocate({
            x1p1 == 0
            x2p1 == 1-2*t1/tcut
            })
            collocate(up1==0)};
    else
        x01 = {tcut == tcut_opt
            tmax == tmax_opt
            icollocate({
            x1p1 == x1p1_opt
            x2p1 == x2p1_opt
            })
            collocate(up1==up1_opt)};
    end

    % Box constraints
    cbox1 = {0.001 <= tcut <= tmax-0.01
        tmax <= 50
        collocate({0 <= x1p1 <= x1max
        -10 <= x2p1 <= 10})};

    % Set up initial conditions in phase p1
    % Initial constraints
    cbnd1 = initial({x1p1 == 0; x2p1 == 1});

    % ODEs and path constraints
    ceq1 = collocate({
        dot(x1p1) == x2p1
        dot(x2p1) == up1});

    % We take advantage of the fact that we've determined that a good place to
    % shift between phases is when x1 reaches x1max, and that x2 must equal 0
    % there (Later, we want the solver to be able to figure this out for
    % itself).
    % Final constraints
    cbnd1 = {cbnd1
        final({x1p1 == x1max; x2p1 == 0})};

    % Using integral gives the integral over the phase of an expression -
    % in this case 0.5 times the square of u.
    % Objective
    objective1 = integrate(0.5*up1.^2);

    setPhase(p2);
    % Initial guess
    if n==5
        x02 = {icollocate({
            x1p2 == 0
            x2p2 == 1-2*t2/tmax
            })
            collocate(up2==0)};
    else
        x02 = {icollocate({
            x1p2 == x1p2_opt
            x2p2 == x2p2_opt
            })
            collocate(up2==up2_opt)};
    end

    % Box constraints
    cbox2 = collocate({0 <= x1p2 <= x1max
        -10 <= x2p2 <= 10});

    % ODEs and path constraints
    ceq2 = collocate({
        dot(x1p2) == x2p2
        dot(x2p2) == up2});

    % x2_i of p2 is already linked to x2_f of p1, but linking it to a constant
    % helps convergence.
    % Final conditions in phase p2.
    cbnd2 = {initial(x2p2 == 0)
        final(x1p2 == 0)
        final(x2p2 == -1)};

    objective2 = integrate(0.5*up2.^2);

    % Link the phases
    link = {final(p1,x1p1) == initial(p2,x1p2)
        final(p1,x2p1) == initial(p2,x2p2)};

Solve the problem

    options = struct;
    options.name = 'Bryson Denham Two Phase';
    objective = objective1+objective2;
    constr = {cbox1, cbnd1, ceq1, cbox2, cbnd2, ceq2, link};
    solution = ezsolve(objective, constr, {x01, x02}, options);
    x1p1_opt = subs(x1p1, solution);
    x2p1_opt = subs(x2p1, solution);
    up1_opt  = subs(up1, solution);
    x1p2_opt = subs(x1p2, solution);
    x2p2_opt = subs(x2p2, solution);
    up2_opt  = subs(up2, solution);
    tcut_opt = subs(tcut, solution);
    tmax_opt = subs(tmax, solution);

Problem type appears to be: con
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Bryson Denham Two Phase        f_k       3.999999993412736800
                                       sum(|constr|)      0.000000023177918609
                              f(x_k) + sum(|constr|)      4.000000016590655100
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv   39 GradEv   37 ConstrEv   37 ConJacEv   37 Iter   34 MinorIter   69
CPU time: 0.062500 sec. Elapsed time: 0.078000 sec. 

Problem type appears to be: con
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Bryson Denham Two Phase        f_k       3.999999995253987500
                                       sum(|constr|)      0.000000000347325270
                              f(x_k) + sum(|constr|)      3.999999995601312800
                                              f(x_0)      3.999999738804261200

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    4 GradEv    2 ConstrEv    2 ConJacEv    2 Iter    1 MinorIter   75
CPU time: 0.046875 sec. Elapsed time: 0.046000 sec. 

end

t = subs(collocate(p1,t1),solution);
t = [t;subs(collocate(p2,t2),solution)];
x1 = subs(collocate(p1,x1p1),solution);
x1 = [x1;subs(collocate(p2,x1p2),solution)];
x2 = subs(collocate(p1,x2p1),solution);
x2 = [x2;subs(collocate(p2,x2p2),solution)];

Plot the result

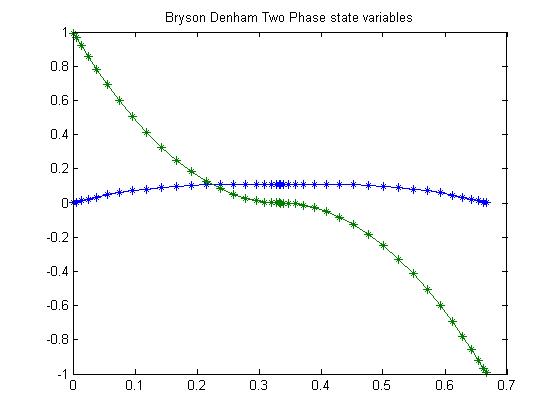
figure(1)
plot(t,x1,'*-',t,x2,'*-');
title('Bryson Denham Two Phase state variables');