Catalyst Mixing
Second-order sensitivities of general dynamic systems with application to optimal control problems. 1999, Vassilios S. Vassiliadis, Eva Balsa Canto, Julio R. Banga
Case Study 6.2: Catalyst mixing
Contents
Problem formulation
This problem considers a plug-flow reactor, packed with two catalysts, involving the reactions
S1 <-> S2 -> S3
The optimal mixing policy of the two catalysts has to be determined in order to maximize the production of species S3. This dynamic optimization problem was originally proposed by Gunn and Thomas (1965), and subsequently considered by Logsdon (1990) and Vassiliadis (1993). The mathematical formulation is
Maximize:
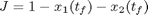
subject to:
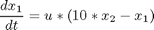
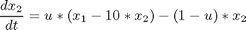
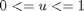
![$$ x(t_0) = [1 \ 0]'$$](xcatalystMixing_eq81187.png)
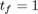
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
toms t p = tomPhase('p', t, 0, 1, 30); setPhase(p); tomStates x1 x2 tomControls u % Initial guess % Note: The guess for tf must appear in the list before expression involving t. x0 = {icollocate({ x1 == 1-0.085*t x2 == 0.05*t }) collocate(u==1-t)}; % Box constraints cbox = {0.9 <= icollocate(x1) <= 1 0 <= icollocate(x2) <= 0.1 0 <= collocate(u) <= 1}; % Boundary constraints cbnd = {initial({x1 == 1; x2 == 0}) final({x1 <= 0.95})}; % ODEs and path constraints ceq = collocate({ dot(x1) == u.*(10*x2-x1) dot(x2) == u.*(x1-10*x2)-(1-u).*x2}); % Objective objective = -1+final(x1)+final(x2);
Solve the problem
options = struct;
options.name = 'Catalyst Mixing';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
t = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
u = subs(collocate(u),solution);
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Catalyst Mixing f_k -0.048059280695325612
sum(|constr|) 0.000000452031697998
f(x_k) + sum(|constr|) -0.048058828663627616
f(x_0) 0.964999999999998080
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 66 ConJacEv 66 Iter 43 MinorIter 247
CPU time: 0.156250 sec. Elapsed time: 0.156000 sec.
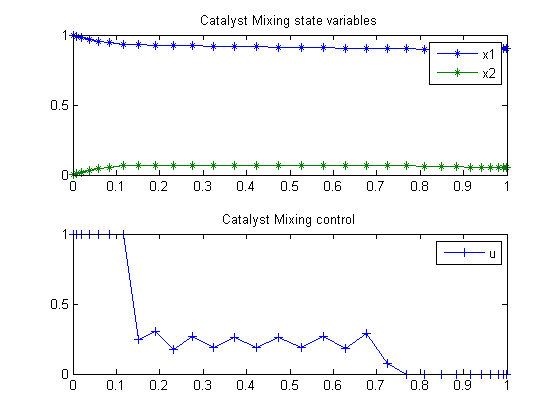
Plot result
subplot(2,1,1) plot(t,x1,'*-',t,x2,'*-'); legend('x1','x2'); title('Catalyst Mixing state variables'); subplot(2,1,2) plot(t,u,'+-'); legend('u'); title('Catalyst Mixing control');