Catalytic Cracking of Gas Oil

Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY

Contents

Problem Formulation

Find theta over t in [0; 0.95] to minimize

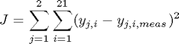
$$ J = \sum_{j=1}^{2} \sum_{i=1}^{21} (y_{j,i} - y_{j,i,meas})^2 $$

subject to:

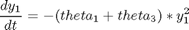
$$ \frac{dy_1}{dt} = -(theta_1+theta_3)*y_1^2 $$

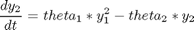
$$ \frac{dy_2}{dt} = theta_1*y_1^2-theta_2*y_2 $$

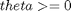
$$ theta >= 0 $$

Where the data is given in the code.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t theta1 theta2 theta3
p = tomPhase('p', t, 0, 0.95, 100);
setPhase(p);

tomStates y1 y2

% Initial guess
x0 = icollocate({
    y1 == 1-(1-0.069)*t/0.95
    y2 == 0.01*t/0.95});

% Box constraints
cbox = {0 <= theta1; 0 <= theta2; 0 <= theta3};

% Various constants and expressions
y1meas = [1.0;0.8105;0.6208;0.5258;0.4345;0.3903;...
    0.3342;0.3034;0.2735;0.2405;0.2283;0.2071;0.1669;...
    0.153;0.1339;0.1265;0.12;0.099;0.087;0.077;0.069];
y2meas = [0;0.2;0.2886;0.301;0.3215;0.3123;0.2716;...
    0.2551;0.2258;0.1959;0.1789;0.1457;0.1198;0.0909...
    ;0.0719;0.0561;0.046;0.028;0.019;0.014;0.010];
tmeas = [0;0.025;0.05;0.075;0.1;0.125;...
    0.15;0.175;0.2;0.225;0.25;0.3;0.35;0.4;...
    0.45;0.5;0.55;0.65;0.75;0.85;0.95];

y1err = atPoints(tmeas,y1) - y1meas;
y2err = atPoints(tmeas,y2) - y2meas;

% ODEs and path constraints
ceq = collocate({
    dot(y1) == -(theta1+theta3)*y1.^2
    dot(y2) == theta1*y1.^2-theta2*y2});

% Objective
objective = sum(y1err.^2)+sum(y2err.^2);

Solve the problem

options = struct;
options.name = 'Catalytic Cracking';
solution = ezsolve(objective, {cbox, ceq}, x0, options);
t  = subs(collocate(t),solution);
y1 = subs(collocate(y1),solution);
y2 = subs(collocate(y2),solution);
theta1 = subs(theta1,solution);
theta2 = subs(theta2,solution);
theta3 = subs(theta3,solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Catalytic Cracking             f_k       0.004326020490939442
                                       sum(|constr|)      0.000000000507606811
                              f(x_k) + sum(|constr|)      0.004326020998546253
                                              f(x_0)      0.165642328947365970

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   38 ConJacEv   38 Iter   29 MinorIter  198
CPU time: 0.671875 sec. Elapsed time: 0.672000 sec.

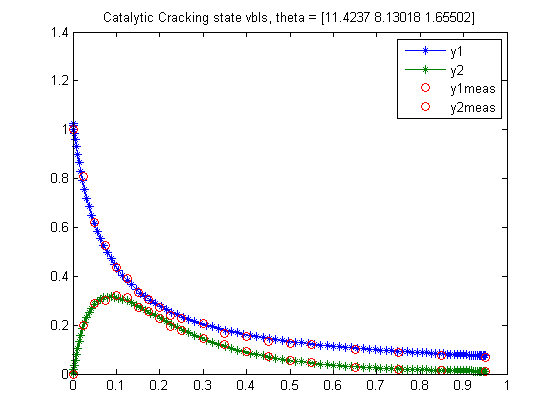
Plot result

figure(1);
tm  = tmeas;  y1m = y1meas; y2m = y2meas;
t1  = theta1; t2  = theta2; t3  = theta3;
plot(t,y1,'*-',t,y2,'*-',tm,y1m,'ro',tm,y2m,'ro');
legend('y1','y2','y1meas','y2meas');
title(sprintf('Catalytic Cracking state vbls, theta = [%g %g %g]',t1,t2,t3));