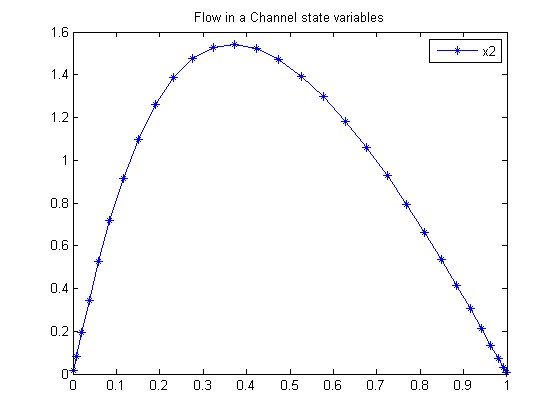
Flow in a Channel

Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY

Contents

Problem Formulation

Find u(t) over t in [0; 1 ] to minimize

$$ J = 0 $$

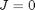
subject to:

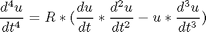
$$ \frac{d^{4}u}{dt^{4}} = R*(\frac{du}{dt}*\frac{d^{2}u}{dt^{2}}-u*\frac{d^{3}u}{dt^{3}}) $$

$$ u_0 = 0 $$

$$ u_1 = 1 $$

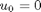
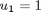
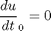
$$ \frac{du}{dt}_0 = 0 $$

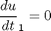
$$ \frac{du}{dt}_1 = 0 $$

$$ R = 10 $$

After some transformation we get this problem:

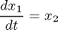
$$ \frac{dx_1}{dt} = x_2 $$

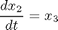
$$ \frac{dx_2}{dt} = x_3 $$

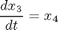
$$ \frac{dx_3}{dt} = x_4 $$

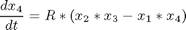
$$ \frac{dx_4}{dt} = R*(x_2*x_3-x_1*x_4) $$

$$ x_1(0) = 0 $$

$$ x_1(1) = 1 $$

$$ x_2(0) = 0 $$

$$ x_2(1) = 0 $$

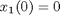
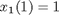
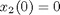
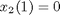
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, 0, 1, 30);
setPhase(p);

tomStates x1 x2 x3 x4

x0 = icollocate({x1 == 3*t.^2 - 2*t.^3
    x2 == 2*t - 6*t.^2
    x3 == t - 12*t
    x4 == -12});

% Boundary constraints
cbnd = {initial({x1 == 0; x2 == 0})
    final({x1 == 1; x2 == 0})};

% Various constants and expressions
R = 10;

% ODEs and path constraints
ceq = collocate({dot(x1) == x2
    dot(x2) == x3; dot(x3) == x4
    dot(x4) == R*(x2.*x3-x1.*x4)});

% Objective
objective = 1; %(feasibility problem)

Solve the problem

options = struct;
options.name = 'Flow in a Channel Steering';
solution = ezsolve(objective, {cbnd, ceq}, x0, options);

% Extract optimal states and controls from solution
t  = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
x3 = subs(collocate(x3),solution);
x4 = subs(collocate(x4),solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Flow in a Channel Steering     f_k       1.000000000000000000
                                       sum(|constr|)      0.000000000858386026
                              f(x_k) + sum(|constr|)      1.000000000858386000
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   11 ConJacEv   11 Iter    8 MinorIter   54
CPU time: 0.062500 sec. Elapsed time: 0.063000 sec.

Plot result

figure(1)
plot(t,x2,'*-');
legend('x2');
title('Flow in a Channel state variables');