Denbigh's System of Reactions

Dynamic Optimization of Batch Reactors Using Adaptive Stochastic Algorithms 1997, Eugenio F. Carrasco, Julio R. Banga

Case Study I: Denbigh's System of Reactions

Contents

Problem description

This optimal control problem is based on the system of chemical reactions initially considered by Denbigh (1958), which was also studied by Aris (1960) and more recently by Luus (1994):

A + B -> X

A + X -> P

X -> Y

X -> Q

where X is an intermediate, Y is the desired product, and P and Q are waste products. This system is described by the following differential equations:

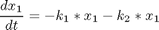
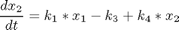
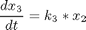
where x1 = [A][B], x2 = [X] and x3 = [Y]. The initial condition is

The rate constants are given by

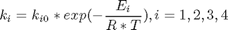
where the values of ki0 and Ei are given by Luus (1994).

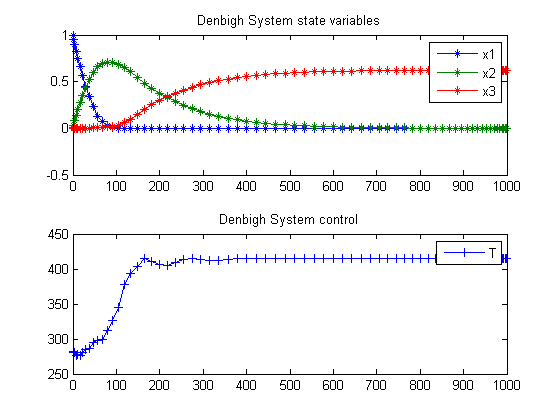
The optimal control problem is to find T(t) (the temperature of the reactor as a function of time) so that the yield of Y is maximized at the end of the given batch time tf. Therefore, the performance index to be maximized is

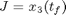
where the batch time tf is specified as 1000 s. The constraints on the control variable (reactor temperature) are

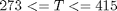
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t

Solve the problem, using a successively larger number collocation points

for n=[25 70]

    p = tomPhase('p', t, 0, 1000, n);
    setPhase(p);
    tomStates x1 x2 x3
    tomControls T

    % Initial guess
    if n==25
        x0 = {icollocate({
            x1 == 1-t/1000;
            x2 == 0.15
            x3 == 0.66*t/1000
            })
            collocate(T==273*(t<100)+415*(t>=100))};
    else
        x0 = {icollocate({
            x1 == x1_init
            x2 == x2_init
            x3 == x3_init
            })
            collocate(T==T_init)};
    end

    % Box constraints
    cbox = {
        0 <= icollocate(x1) <= 1
        0 <= icollocate(x2) <= 1
        0 <= icollocate(x3) <= 1
        273 <= collocate(T) <= 415};

    % Boundary constraints
    cbnd = initial({x1 == 1; x2 == 0
        x3 == 0});

    % Various constants and expressions
    ki0 = [1e3; 1e7; 10; 1e-3];
    Ei  = [3000; 6000; 3000; 0];
    ki4 = ki0(4)*exp(-Ei(4)./T);
    ki3 = ki0(3)*exp(-Ei(3)./T);
    ki2 = ki0(2)*exp(-Ei(2)./T);
    ki1 = ki0(1)*exp(-Ei(1)./T);

    % ODEs and path constraints
    ceq = collocate({
        dot(x1) == -ki1.*x1-ki2.*x1
        dot(x2) == ki1.*x1-(ki3+ki4).*x2
        dot(x3) == ki3.*x2});

    % Objective
    objective = -final(x3);

Solve the problem

    options = struct;
    options.name = 'Denbigh System';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
    x1_init  = subs(x1,solution);
    x2_init  = subs(x2,solution);
    x3_init  = subs(x3,solution);
    T_init   = subs(T,solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Denbigh System                 f_k      -0.632418776163711120
                                       sum(|constr|)      0.000024152175629419
                              f(x_k) + sum(|constr|)     -0.632394623988081660
                                              f(x_0)     -0.659999999999999250

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   26 ConJacEv   26 Iter   19 MinorIter 1057
CPU time: 0.171875 sec. Elapsed time: 0.172000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Denbigh System                 f_k      -0.621639303673750640
                                       sum(|constr|)      0.000000206291432199
                              f(x_k) + sum(|constr|)     -0.621639097382318480
                                              f(x_0)     -0.632419741360300770

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   10 ConJacEv   10 Iter    9 MinorIter  265
CPU time: 0.359375 sec. Elapsed time: 0.360000 sec. 

end

t  = collocate(subs(t,solution));
x1 = collocate(x1_init);
x2 = collocate(x2_init);
x3 = collocate(x3_init);
T  = collocate(T_init);

Plot result

subplot(2,1,1)
plot(t,x1,'*-',t,x2,'*-',t,x3,'*-');
legend('x1','x2','x3');
title('Denbigh System state variables');

subplot(2,1,2)
plot(t,T,'+-');
legend('T');
title('Denbigh System control');