Optimal Drug Scheduling for Cancer Chemotherapy

Dynamic optimization of bioprocesses: efficient and robust numerical strategies 2003, Julio R. Banga, Eva Balsa-Cantro, Carmen G. Moles and Antonio A. Alonso

Case Study III: Optimal Drug Scheduling for Cancer Chemotherapy

Contents

Problem description

Many researches have devoted their efforts to determine whether current methods for drugs administration during cancer chemotherapy are optimal, and if alternative regimens should be considered. Martin (1992) considered the interesting problem of determining the optimal cancer drug scheduling to decrease the size of a malignant tumor as measured at some particular time in the future. The drug concentration must be kept below some level throughout the treatment period and the cumulative (toxic) effect of the drug must be kept below the ultimate tolerance level. Bojkov et al. (1993) and Luus et al. (1995) also studied this problem using direct search optimization. More recently, Carrasco and Banga (1997) have applied stochastic techniques to solve this problem, obtaining better results (Carrasco & Banga 1998). The mathematical statement of this dynamic optimization problem is: Find u(t) over t in [t0; tf ] to maximize:

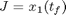
subject to:

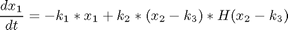
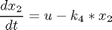
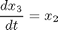
where the tumor mass is given by N = 10^12 * exp (-x1) cells, x2 is the drug concentration in the body in drug units [D] and x3 is the cumulative effect of the drug. The parameters are taken as k1 = 9.9e-4 days, k2 = 8.4e-3 days-1 [De-1], k3 = 10 [De-1], and k4 = 0.27 days-1. The initial state considered is:

where,

H(x2-k3) = 1 if x2 >= k3 or 0 if x2 < k3

and the final time tf = 84 days. The optimization is subject to the following constraints on the drug delivery (control variable):

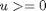
There are the following path constraints on the state variables:

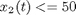
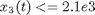
Also, there should be at least a 50% reduction in the size of the tumor every three weeks, so that the following point constraints must be considered:

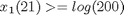
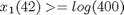
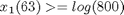
State number 3 is converted to an integral constraints in the formulation.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t

nn = [20 40 120];

for i = 1:length(nn)

    n = nn(i);
    p = tomPhase('p', t, 0, 84, n);
    setPhase(p);

    tomStates x1 x2
    tomControls u

    % Initial guess
    if i==1
        x0 = {icollocate(x2 == 10)
            collocate(u == 20)};
    else
        x0 = {icollocate({x1 == x1opt; x2 == x2opt})
            collocate(u == uopt)};
    end

    % Box constraints
    cbox = {
        0 <= mcollocate(x1)
        0 <= mcollocate(x2) <= 50
        0 <= collocate(u)   <= 80};

    % Boundary constraints
    cbnd = initial({x1 == log(100); x2 == 0});

    % ODEs and path constraints
    k1 = 9.9e-4; k2 = 8.4e-3;
    k3 = 10;     k4 = 0.27;
    ceq = {collocate({
        dot(x1) == -k1*x1+k2*max(x2-k3,0)
        dot(x2) == u-k4*x2})
        % Point-wise conditions
        atPoints([21;42;63],x1) >= log([200;400;800])
        % Integral constr.
        integrate(x2) == 2.1e3};

    % Objective
    objective = -final(x1);

Solve the problem

    options = struct;
    options.name = 'Drug Scheduling';
    options.solver = 'multiMin';
    options.xInit = 130-n;
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

    x1opt = subs(x1, solution);
    x2opt = subs(x2, solution);
    uopt  = subs(u, solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Drug Scheduling                f_k     -16.921534390056696000
                                       sum(|constr|)      0.000000000000745242
                              f(x_k) + sum(|constr|)    -16.921534390055950000
                                              f(x_0)   -171.672308625670670000

Solver: multiMin with local solver snopt.  EXIT=0.  INFORM=1.
Find local optima using multistart local search
Did 110 local tries. Found 79 local minima

FuncEv    1 ConstrEv   21 ConJacEv   20 Iter   10 MinorIter  246
CPU time: 4.828125 sec. Elapsed time: 4.922000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Drug Scheduling                f_k     -17.267425658711193000
                                       sum(|constr|)      0.000000000001426355
                              f(x_k) + sum(|constr|)    -17.267425658709769000
                                              f(x_0)    369.788912036584410000

Solver: multiMin with local solver snopt.  EXIT=0.  INFORM=1.
Find local optima using multistart local search
Did 90 local tries. Found 88 local minima

FuncEv    1 ConstrEv   39 ConJacEv   38 Iter   19 MinorIter  802
CPU time: 12.406250 sec. Elapsed time: 12.485000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Drug Scheduling                f_k     -17.407146220453011000
                                       sum(|constr|)      0.000000000017067115
                              f(x_k) + sum(|constr|)    -17.407146220435944000
                                              f(x_0)    -17.267425658711261000

Solver: multiMin with local solver snopt.  EXIT=0.  INFORM=1.
Find local optima using multistart local search
Did 10 local tries. Found 9 local minima

FuncEv    1 ConstrEv   69 ConJacEv   68 Iter   25 MinorIter  777
CPU time: 31.593750 sec. Elapsed time: 31.765000 sec. 

end

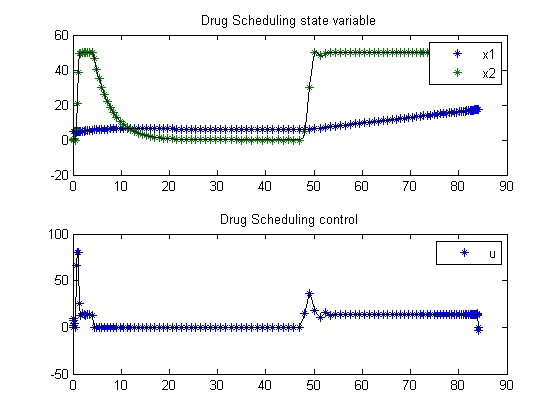
Plot result

subplot(2,1,1)
ezplot([x1;x2]);
legend('x1','x2');
title('Drug Scheduling state variable');

subplot(2,1,2)
ezplot(u);
legend('u');
title('Drug Scheduling control');