MK2 5-Link robot

Singular time-optimal of the MK2 5-Link robot. Implementation without mass matrix inversion.

Contents

Problem description

The dynamic model of the MK2 robot was generated automatically by AUTOLEV that produces Fortran 77 code: http://www.autolev.com/

The transfer to matlab code was performed partly automatically using

 1) to_f90: http://users.bigpond.net.au/amiller/
 2) f2matlab.m: http://www.mathworks.com/matlabcentral/fileexchange/5260

Programmer: Gerard Van Willigenburg (Wageningen University)

% Copyright (c) 2009-2009 by Tomlab Optimization Inc.

Problem setup

toms t tf % Free final time

p = tomPhase('p', t, 0, tf, 20);
setPhase(p);

global AP4AD
AP4AD = true; % Work-around to get more efficient code for this particular case.

% Dimension state and control vector
np = 5; nx = 2*np; nu = np;

% Define the state and control vector
tomStates a1 a2 a3 a4 a5 w1 w2 w3 w4 w5
alpha = [a1; a2; a3; a4; a5];
omega = [w1; w2; w3; w4; w5];
tomControls u1 u2 u3 u4 u5
u     = [u1; u2; u3; u4; u5];

% Initial and terminal states
znp    = zeros(np,1);
alphaf = [0.975; 0.975; 0; 0; 0.975];

% Maximum values controls
umax = [15; 10; 5; 5; 5];

% Initial guess
x0 = {tf==0.8;
    icollocate({alpha == alphaf; omega == znp})
    collocate({u == 0})};

% Box constraints
cbox = {0.7 <= tf <= 0.9;
    collocate({-umax <= u <= umax})};

% Boundary constraints
cbnd = {initial({alpha == znp; omega == znp})
    final({alpha == alphaf; omega == znp})};

% Compute mass matrix
[mass, rhs] = fiveLinkMK2Robotdyn([alpha; omega], u);

% Equality differential equation constraints
ceq = collocate({dot(alpha) == omega; mass*dot(omega) == rhs});

% Objective
objective = tf;

Solve the problem

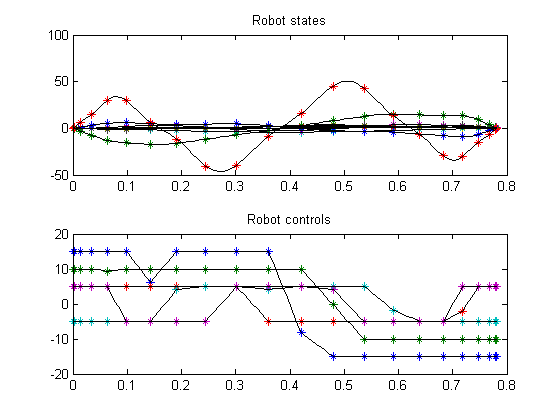
options = struct;
options.use_d2c = 0;
options.use_H   = 0;
options.type = 'lpcon';
options.name = 'Five Link MK2 Robot';
options.derivatives = 'automatic';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

% Plot intermediate result
subplot(2,1,1);
ezplot([alpha; omega]);
title('Robot states');

subplot(2,1,2);
ezplot(u);
title('Robot controls');

clear AP4AD

===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Five Link MK2 Robot            f_k       0.781121378222925930
                                       sum(|constr|)      0.000037255049196879
                              f(x_k) + sum(|constr|)      0.781158633272122760
                                              f(x_0)      0.800000000000000040

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
MAD TB Automatic Differentiation estimating: gradient and constraint gradient

FuncEv    1 ConstrEv  398 ConJacEv  138 Iter  118 MinorIter 1175
CPU time: 201.031250 sec. Elapsed time: 155.297000 sec.