Food Sterilization

Contents

Problem description

Simplified version of the sterilization problem considered in the paper: Z.S. Chalabi, L.G. van Willigenburg, G. van Straten, 1999, Robust optimal receding horizon control of the thermal sterilization of canned food, Journal of Food Engineering, 40, pp. 207-218.

Programmers: Gerard Van Willigenburg (Wageningen University) Willem De Koning (retired from Delft University of Technology)

% Copyright (c) 2009-2009 by Tomlab Optimization Inc.

Problem setup

% Array with consecutive number of collocation points
narr = [20 30 40];

toms t;
tf = 1500; % Fixed final time

for n=narr

    p = tomPhase('p', t, 0, tf, n);
    setPhase(p)

    tomStates x1 x2 x3 x4
    tomControls u1

    % Initial & terminal states
    xi = [20; 20;   0; 0];
    xf = [40;  0; 100; 0];

    % Initial guess
    if n==narr(1)
        x0 = {icollocate({x1 == xi(1); x2 == xi(2)
            x3 == xi(3); x4 == xi(4)})
            collocate({u1 == 50})};
    else
        x0 = {icollocate({x1 == xopt1; x2 == xopt2
            x3 == xopt3; x4 == xopt4})
            collocate({u1 == uopt1})};
    end

    % Box constraints
    cbox = {0 <= collocate(u1) <= 50};

    % Boundary constraints
    cbnd = {initial({x1 == xi(1); x2 == xi(2); x3 == xi(3); x4 == xi(4)})};

    % ODEs and path constraints
    pv  = [0.01; 0.005; 0.01; 20; 10; 121.11; 25.56; 121.11];
    dx1 = pv(1)*(x2-x1);
    dx2 = pv(2)*(pv(4)-x2)+pv(3)*u1;
    dx3 = exp(log(10)/pv(5)*(x1-pv(6)));
    dx4 = exp(log(10)/pv(7)*(x1-pv(8)));

    ceq = collocate({
        dot(x1) == dx1; dot(x2) == dx2
        dot(x3) == dx3; dot(x4) == dx4});

    % Objective
    objective = final(x4)+final((x3-100)^2)+final((x1-40)^2);

Solve the problem

    options = struct;
    options.name = 'Food Sterilization';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

    xopt1 = subs(x1,solution);
    xopt2 = subs(x2,solution);
    xopt3 = subs(x3,solution);
    xopt4 = subs(x4,solution);
    uopt1 = subs(u1,solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Food Sterilization             f_k     280.311099407259460000
                                       sum(|constr|)      0.000000001761330483
                              f(x_k) + sum(|constr|)    280.311099409020810000
                                              f(x_0)  -1200.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   63 ConJacEv   63 Iter   52 MinorIter  308
CPU time: 0.140625 sec. Elapsed time: 0.140000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Food Sterilization             f_k     271.918781767461040000
                                       sum(|constr|)      0.000000000005433066
                              f(x_k) + sum(|constr|)    271.918781767466500000
                                              f(x_0) -11319.688900592708000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   20 ConJacEv   20 Iter   17 MinorIter  139
CPU time: 0.093750 sec. Elapsed time: 0.094000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Food Sterilization             f_k     272.292678100737250000
                                       sum(|constr|)      0.000000003270547055
                              f(x_k) + sum(|constr|)    272.292678104007790000
                                              f(x_0) -11328.081218232532000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   29 ConJacEv   29 Iter   26 MinorIter  203
CPU time: 0.203125 sec. Elapsed time: 0.203000 sec. 

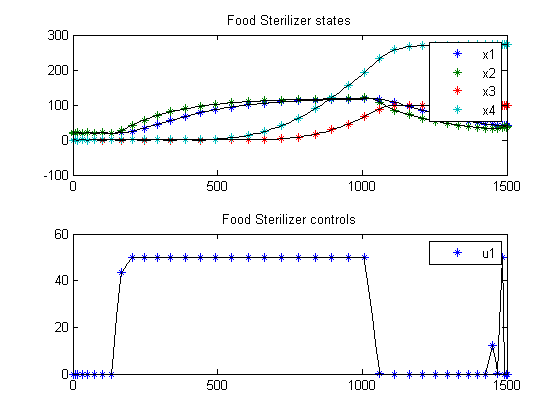
end

figure(1)
subplot(2,1,1);
ezplot([x1; x2; x3; x4]); legend('x1','x2','x3','x4');
title('Food Sterilizer states');

subplot(2,1,2);
ezplot(u1); legend('u1');
title('Food Sterilizer controls');