Global Dynamic System

Deterministic Global Optimization of Nonlinear Dynamic Systems, Youdong Lin and Mark A. Stadtherr, Department of Chemical and Biomolecular Engineering, University of Notre Dame

Contents

Problem Description

Find u over t in [0; 1 ] to minimize:

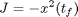
$$ J = -x^2(t_f) $$

subject to:

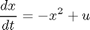
$$ \frac{dx}{dt} = -x^2+u $$

$$ x(t_0) = 9 $$

$$ -5 <= u <= 5 $$

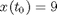
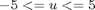
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, 0, 1, 20);
setPhase(p);

tomStates x
tomControls u

% Box constraints, bounds and odo
c = {-10 <= icollocate(x) <= 10
    -5  <= collocate(u)  <= 5
    initial(x == 9)
    collocate(dot(x) == -x.^2+u)};

Solve the problem

options = struct;
options.name = 'Global Dynamic System';
Prob = sym2prob('con',-final(x)^2, c, [], options);
Prob.xInit = 20;
Result = tomRun('multiMin', Prob, 1);
solution = getSolution(Result);
t = subs(collocate(t),solution);
x = subs(collocate(x),solution);
u = subs(collocate(u),solution);

===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Global Dynamic System          f_k      -8.232621699201864400
                                       sum(|constr|)      0.000000000001350919
                              f(x_k) + sum(|constr|)     -8.232621699200514300
                                              f(x_0)   -722.770548126228160000

Solver: multiMin with local solver snopt.  EXIT=0.  INFORM=1.
Find local optima using multistart local search
Did 20 local tries. Found 2 local minima

FuncEv   31 GradEv   29 ConstrEv   29 ConJacEv   29 Iter   17 MinorIter  103
CPU time: 0.937500 sec. Elapsed time: 0.953000 sec.

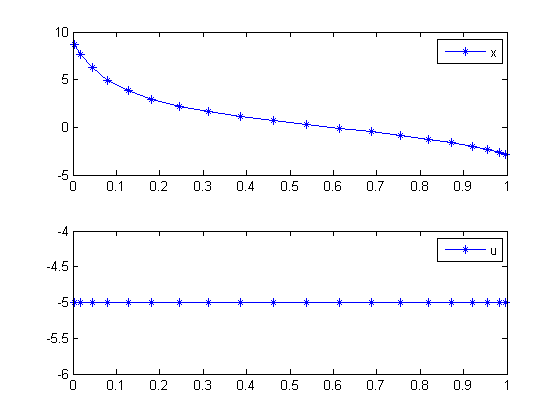
Plot result

figure(1);
subplot(2,1,1);
plot(t,x,'*-');
legend('x');

subplot(2,1,2);
plot(t,u,'*-');
legend('u');