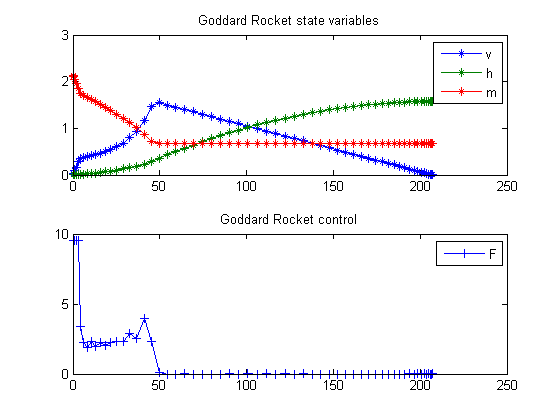
Goddard Rocket, Maximum Ascent, Final time free, Singular solution

Example 7.2 (i) from the paper: H. Maurer, "Numerical solution of singular control problems using multiple shooting techniques", Journal of Optimization Theory and Applications, Vol. 18, No. 2, 1976, pp. 235-257

L.G. van Willigenburg, W.L. de Koning

Copyright (c) 2007-2009 by Tomlab Optimization Inc.

Contents

Problem setup

toms t tf

% Parameters
alpha = 0.01227; beta = 0.145e-3;

c  = 2060;    g0 = 9.81;
r0 = 6.371e6; r02=r0*r0;
m0 = 214.839; mf = 67.9833;
Fm = 9.525515;

Solve the problem, using a successively larger number collocation points

for n=[20 40 60]

    p = tomPhase('p', t, 0, tf, n);
    setPhase(p);
    tomStates h v m
    tomControls F

    % Initial guess
    if n==20
        x0 = {tf==250
            icollocate({v == 0; h == 0
            m == m0})
            collocate(F == Fm)};
    else
        x0 = {tf == tfopt
            icollocate({v == vopt; h == hopt
            m == mopt})
            collocate(F == Fopt)};
    end

    % Box constraints
    cbox = {100 <= tf <= 300
        icollocate({0 <= v; 0 <= h
        mf <= m <= m0
        0 <= F <= Fm})};

    % Boundary constraints
    cbnd = {initial({v == 0; h == 0; m == m0})
        final({v==0; m == mf})};

    D = alpha*v.^2.*exp(-beta*h);
    g = g0; % or g0*r02./(r0+h).^2;

    % ODEs and path constraints
    ceq = collocate({dot(h) == v
        m*dot(v) == F*c-D-g*m
        dot(m) == -F});

    % Objective
    objective = -1e-4*final(h);

    %% Solve the problem
    options = struct;
    options.name = 'Goddard Rocket 1';
    options.Prob.SOL.optPar(30) = 30000;
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

    % Optimal v and more to use as starting guess
    vopt = subs(v, solution);
    hopt = subs(h, solution);
    mopt = subs(m, solution);
    Fopt = subs(F, solution);
    tfopt = subs(tf, solution);
end

t = subs(collocate(t),solution);
v = subs(collocate(vopt),solution);
h = subs(collocate(hopt),solution);
m = subs(collocate(mopt),solution);
F = subs(collocate(Fopt),solution);

Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Goddard Rocket 1               f_k     -15.580049356479115000
                                       sum(|constr|)      0.000028635866519332
                              f(x_k) + sum(|constr|)    -15.580020720612596000
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  217 ConJacEv  216 Iter   45 MinorIter 1278
CPU time: 0.640625 sec. Elapsed time: 1.344000 sec. 
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Goddard Rocket 1               f_k     -15.718139470103905000
                                       sum(|constr|)      0.043635004313635782
                              f(x_k) + sum(|constr|)    -15.674504465790269000
                                              f(x_0)    -15.580049356479037000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  237 ConJacEv  235 Iter   34 MinorIter  919
CPU time: 1.031250 sec. Elapsed time: 1.031000 sec. 
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Goddard Rocket 1               f_k     -15.731752553138087000
                                       sum(|constr|)      0.000724004045428859
                              f(x_k) + sum(|constr|)    -15.731028549092658000
                                              f(x_0)    -15.718139470103864000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  271 ConJacEv  270 Iter   51 MinorIter 4625
CPU time: 3.187500 sec. Elapsed time: 3.234000 sec. 

Plot result

subplot(2,1,1)
plot(t,v/1e3,'*-',t,h/1e5,'*-',t,m/1e2,'*-');
legend('v','h','m');
title('Goddard Rocket state variables');

subplot(2,1,2)
plot(t,F,'+-');
legend('F');
title('Goddard Rocket control');