High Dimensional Control

Problem 7: DYNOPT User's Guide version 4.1.0

M. Cizniar, M. Fikar, M. A. Latifi, MATLAB Dynamic Optimisation Code DYNOPT. User's Guide, Technical Report, KIRP FCHPT STU Bratislava, Slovak Republic, 2006.

Contents

Problem description

Find u over t in [0; 0.2 ] to minimize

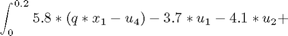
$$ \int_0^{0.2} 5.8*(q*x_1-u_4)-3.7*u_1-4.1*u_2+ $$

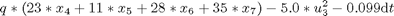
$$ q*(23*x_4+11*x_5+28*x_6+35*x_7)-5.0*u_3^2-0.099 \mathrm{d}t $$

subject to:

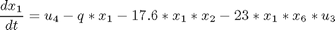
$$ \frac{dx_1}{dt} = u_4-q*x_1-17.6*x_1*x_2-23*x_1*x_6*u_3 $$

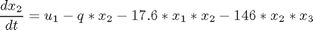
$$ \frac{dx_2}{dt} = u_1-q*x_2-17.6*x_1*x_2-146*x_2*x_3 $$

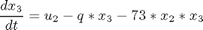
$$ \frac{dx_3}{dt} = u_2-q*x_3-73*x_2*x_3 $$

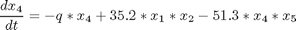
$$ \frac{dx_4}{dt} = -q*x_4+35.2*x_1*x_2-51.3*x_4*x_5 $$

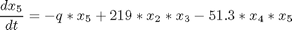
$$ \frac{dx_5}{dt} = -q*x_5+219*x_2*x_3-51.3*x_4*x_5 $$

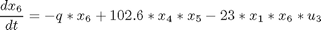
$$ \frac{dx_6}{dt} = -q*x_6+102.6*x_4*x_5-23*x_1*x_6*u_3 $$

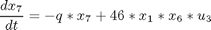
$$ \frac{dx_7}{dt} = -q*x_7+46*x_1*x_6*u_3 $$

where

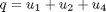
$$ q = u_1+u_2+u_4 $$

$$ x(0) = [0.1883 \ 0.2507 \ 0.0467 \ 0.0899 \ 0.1804 \ 0.1394 \ 0.1046]' $$

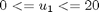
$$ 0 <= u_1 <= 20 $$

$$ 0 <= u_2 <= 6 $$

$$ 0 <= u_3 <= 4 $$

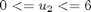
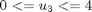
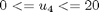
$$ 0 <= u_4 <= 20 $$

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, 0, 0.2, 20);
setPhase(p);

tomStates x1 x2 x3 x4 x5 x6 x7
tomControls u1 u2 u3 u4

x = [x1; x2; x3; x4; x5; x6; x7];
u = [u1; u2; u3; u4];

x0i = [0.1883;0.2507;0.0467;0.0899;0.1804;0.1394;0.1046];
x0 = icollocate({x1==x0i(1),x2==x0i(2),x3==x0i(3),x4==x0i(4),x5==x0i(5),x6==x0i(6),x7==x0i(7)});

% Box constraints and boundary
uL = zeros(4,1); uU = [20;6;4;20];
cbb = {collocate(uL <= u <= uU)
    initial(x == x0i)};

% ODEs and path constraints
q = u(1)+u(2)+u(4);
ceq = collocate({
    dot(x1) == u4-q.*x1-17.6*x1.*x2-23*x1.*x6.*u3;
    dot(x2) == u1-q.*x2-17.6*x1.*x2-146*x2.*x3;
    dot(x3) == u2-q.*x3-73*x2.*x3;
    dot(x4) == -q.*x4+35.2*x1.*x2-51.3*x4.*x5;
    dot(x5) == -q.*x5+219*x2.*x3-51.3*x4.*x5;
    dot(x6) == -q.*x6+102.6*x4.*x5-23*x1.*x6.*u3;
    dot(x7) == -q.*x7+46*x1.*x6.*u3});

% Objective
objective = integrate(-(5.8*(q.*x1-u4)-3.7*u1-4.1*u2+...
    q.*(23*x4+11*x5+28*x6+35*x7)-5.0*u3.^2-0.099));

Solve the problem

options = struct;
options.name = 'High Dim Control';
solution = ezsolve(objective, {cbb, ceq}, x0, options);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: High Dim Control               f_k     -21.834326989504241000
                                       sum(|constr|)      0.000000000012388114
                              f(x_k) + sum(|constr|)    -21.834326989491853000
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  101 ConJacEv  101 Iter   99 MinorIter  488
CPU time: 1.109375 sec. Elapsed time: 1.109000 sec.

Plot result

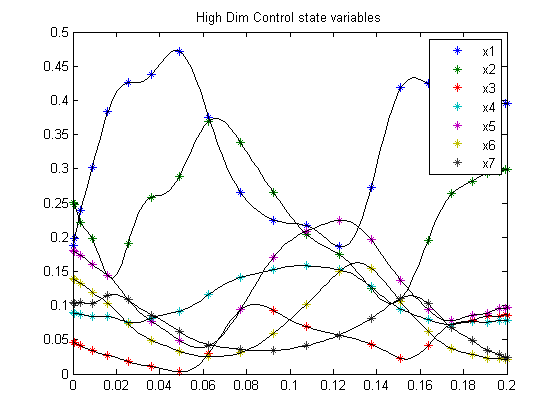
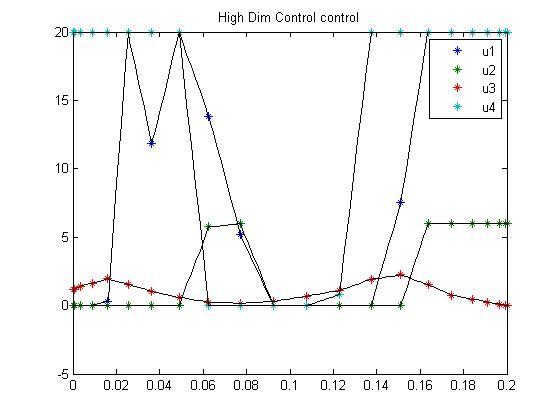
figure(1)
ezplot(x);
legend('x1','x2','x3','x4','x5','x6','x7');
title('High Dim Control state variables');

figure(2)
ezplot(u);
legend('u1','u2','u3','u4');
title('High Dim Control control');