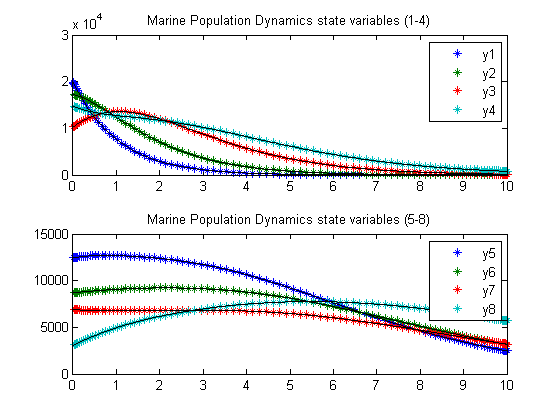
Marine Population Dynamics
Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY
Contents
Problem Formulation
Find m and g over t in [0; 10] to minimize
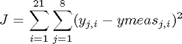
subject to:
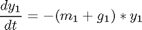
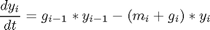
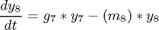
Where the data is given in the code.
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
t = tom('t'); m = tom('m',8,1); g = tom('g',7,1); % Various constants and expressions ymeas = [... 20000 17000 10000 15000 12000 9000 7000 3000 12445 15411 13040 13338 13484 8426 6615 4022 7705 13074 14623 11976 12453 9272 6891 5020 4664 8579 12434 12603 11738 9710 6821 5722 2977 7053 11219 11340 13665 8534 6242 5695 1769 5054 10065 11232 12112 9600 6647 7034 943 3907 9473 10334 11115 8826 6842 7348 581 2624 7421 10297 12427 8747 7199 7684 355 1744 5369 7748 10057 8698 6542 7410 223 1272 4713 6869 9564 8766 6810 6961 137 821 3451 6050 8671 8291 6827 7525 87 577 2649 5454 8430 7411 6423 8388 49 337 2058 4115 7435 7627 6268 7189 32 228 1440 3790 6474 6658 5859 7467 17 168 1178 3087 6524 5880 5562 7144 11 99 919 2596 5360 5762 4480 7256 7 65 647 1873 4556 5058 4944 7538 4 44 509 1571 4009 4527 4233 6649 2 27 345 1227 3677 4229 3805 6378 1 20 231 934 3197 3695 3159 6454 1 12 198 707 2562 3163 3232 5566]; tmeas = 0:0.5:10; % Box constraints cbox = { 0 <= m 0 <= g };
Solve the problem, using a successively larger number collocation points
for n=[20 100]
p = tomPhase('p', t, 0, 10, n, [], 'gauss'); setPhase(p); y = tomState('y',8,1); % Initial guess if n == 20 x0 = {m==0; g==0; icollocate(y == ymeas(1,:)')}; else x0 = {m==mopt; g==gopt icollocate(y == yopt)}; end yerr = sum(sum((atPoints(tmeas,y) - ymeas).^2)); % ODE ceq = collocate( ... dot(y) == [0; g].*[0; y(1:7)] - (m+[g;0]).*y ... );
Solve the problem
options = struct;
options.name = 'Marine Population Dynamics';
solution = ezsolve(yerr/1e5, {cbox, ceq}, x0, options);
% Optimal y, m and g - use as starting guess
yopt = subs(y, solution);
mopt = subs(m, solution);
gopt = subs(g, solution);
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Marine Population Dynamics f_k 197.465297161295890000
sum(|constr|) 0.000000005660280022
f(x_k) + sum(|constr|) 197.465297166956160000
f(x_0) 64163.920000000086000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 23 ConJacEv 23 Iter 22 MinorIter 247
CPU time: 0.187500 sec. Elapsed time: 0.156000 sec.
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Marine Population Dynamics f_k 197.465297160946650000
sum(|constr|) 0.000005972538135834
f(x_k) + sum(|constr|) 197.465303133484780000
f(x_0) -86682.190942838643000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 10 ConJacEv 9 Iter 2 MinorIter 672
CPU time: 2.109375 sec. Elapsed time: 1.797000 sec.
end
Plot result
subplot(2,1,1) ezplot(y(1:4)); legend('y1','y2','y3','y4'); title('Marine Population Dynamics state variables (1-4)'); subplot(2,1,2) ezplot(y(5:8)); legend('y5','y6','y7','y8'); title('Marine Population Dynamics state variables (5-8)');