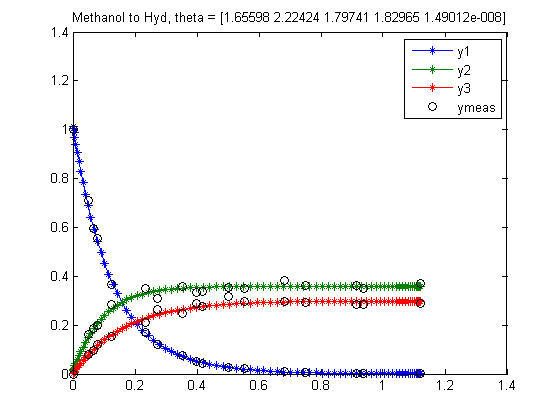
Methanol to Hydrocarbons

Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY

Contents

Problem Formulation

Find theta over t in [0; 1.122] to minimize

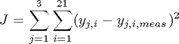
subject to:

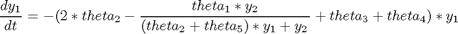
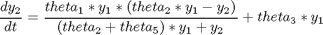
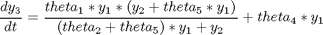
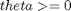
Where the data is given in the code.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t theta1 theta2 theta3 theta4 theta5

% Various constants and expressions
y1meas = [0.7085;0.5971;0.5537;0.3684;0.1712;...
    0.1198;0.0747;0.0529;0.0415;0.0261;0.0208;...
    0.0085;0.0053;0.0019;0.0018];
y2meas = [0.1621;0.1855;0.1989;0.2845;0.3491;...
    0.3098;0.3576;0.3347;0.3388;0.3557;0.3483;...
    0.3836;0.3611;0.3609;0.3485];
y3meas = [0.0811;0.0965;0.1198;0.1535;0.2097;...
    0.2628;0.2467;0.2884;0.2757;0.3167;0.2954;...
    0.295;0.2937;0.2831;0.2846];
tmeas = [0.05;0.065;0.08;0.123;0.233;0.273;...
    0.354;0.397;0.418;0.502;0.553;...
    0.681;0.75;0.916;0.937];

Solve the problem, using a successively larger number collocation points

for n=[20 80]

    p = tomPhase('p', t, 0, 1.122, n);
    setPhase(p);

    tomStates y1 y2 y3

    % Initial guess
    if n == 20
        x0 = {theta1 == 1; theta2 == 1
            theta3 == 1; theta4 == 1
            theta5 == 1
            icollocate({
            y1 == 1-(1-0.0006)*t/1.122
            y2 == 0.3698*t/1.122
            y3 == 0.2899*t/1.122})};
    else
        x0 = {theta1 == theta1opt; theta2 == theta2opt
            theta3 == theta3opt; theta4 == theta4opt
            theta5 == theta5opt
            icollocate({
            y1 == y1opt
            y2 == y2opt
            y3 == y3opt})};
    end

    % Box constraints
    cbox = {sqrt(eps) <= theta1; sqrt(eps) <= theta2
        sqrt(eps) <= theta3; sqrt(eps) <= theta4
        sqrt(eps) <= theta5};

    y1err = sum((atPoints(tmeas,y1) - y1meas).^2);
    y2err = sum((atPoints(tmeas,y2) - y2meas).^2);
    y3err = sum((atPoints(tmeas,y3) - y3meas).^2);

    % Start and end points cannot be interpolated
    y1end = (1-initial(y1)).^2 + (0.0006-final(y1))^2;
    y2end = (0-initial(y2)).^2 + (0.3698-final(y2))^2;
    y3end = (0-initial(y3)).^2 + (0.2899-final(y3))^2;

    % ODEs and path constraints
    ceq = collocate({
        dot(y1) == -(2*theta2-(theta1*y2)./((theta2+theta5)*y1+y2)+theta3+theta4).*y1
        dot(y2) == (theta1*y1.*(theta2*y1-y2))./((theta2+theta5)*y1+y2)+theta3*y1
        dot(y3) == (theta1*y1.*(y2+theta5*y1))./((theta2+theta5)*y1+y2)+theta4*y1});

    % Objective
    objective = y1err+y2err+y3err+y1end+y2end+y3end;

Solve the problem

    options = struct;
    options.name = 'Methanol to Hydrocarbons';
    solution = ezsolve(objective, {cbox, ceq}, x0, options);

    % Optimal x, theta for starting point
    y1opt = subs(y1, solution);
    y2opt = subs(y2, solution);
    y3opt = subs(y3, solution);
    theta1opt = subs(theta1, solution);
    theta2opt = subs(theta2, solution);
    theta3opt = subs(theta3, solution);
    theta4opt = subs(theta4, solution);
    theta5opt = subs(theta5, solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Methanol to Hydrocarbons       f_k       0.008301664004164877
                                       sum(|constr|)      0.000000001050750270
                              f(x_k) + sum(|constr|)      0.008301665054915147
                                              f(x_0)     -0.959232294294470210

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   42 ConJacEv   42 Iter   41 MinorIter   71
CPU time: 0.140625 sec. Elapsed time: 0.141000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Methanol to Hydrocarbons       f_k       0.008301663998482312
                                       sum(|constr|)      0.000000518174023202
                              f(x_k) + sum(|constr|)      0.008302182172505513
                                              f(x_0)     -5.007954925995837100

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    3 ConJacEv    3 Iter    1 MinorIter  195
CPU time: 0.156250 sec. Elapsed time: 0.156000 sec. 

end

t  = subs(collocate(t),solution);
y1 = collocate(y1opt);
y2 = collocate(y2opt);
y3 = collocate(y3opt);
t1 = subs(theta1,solution);
t2 = subs(theta2,solution);
t3 = subs(theta3,solution);
t4 = subs(theta4,solution);
t5 = subs(theta5,solution);

Plot result

figure(1);
tm  = [0;tmeas;1.122];
y1m = [1;y1meas;0.0006];
y2m = [0;y2meas;0.3698];
y3m = [0;y3meas;0.2899];
plot(t,y1,'*-',t,y2,'*-',t,y3,'*-',tm,y1m,'ko',tm,y2m,'ko',tm,y3m,'ko');
legend('y1','y2','y3','ymeas');
title(sprintf('Methanol to Hyd, theta = [%g %g %g %g %g]',t1,t2,t3,t4,t5));