Min Energy Orbit Transfer

Contents

Problem description

Minimum energy orbit transfer of a spacecraft with limited variable thrust.

From the paper: Low thrust, high-accuracy trajectory optimization, I. Michael Ross, Qi Gong and Pooya Sekhavat.

Programmers: Li Jian (Beihang University)

% Copyright (c) 2009-2009 by Tomlab Optimization Inc.

Problem setup

% Array with consecutive number of collocation points
narr = [40 120];

toms t;
toms tf;
t0 = 0;
tfmax = 57;

for n=narr

    %p = tomPhase('p', t, 0, tf-t0, n, [], 'cheb');
    p = tomPhase('p', t, 0, tf-t0, n);
    setPhase(p)

    tomStates r theta vr vt
    tomControls ur ut

    % Parameters
    r0 = 1; theta0 = 0; vr0 = 0; vt0 = 1;
    rf = 4;             vrf = 0; vtf = 0.5;
    umax = 0.01;

    % Initial state
    xi=[r0; theta0; vr0; vt0];

    % Initial guess
    if n==narr(1)
        x0 = {tf == 57;
            icollocate({r == xi(1); theta == xi(2); vr == xi(3); vt == xi(4)})
            collocate({ur == 0; ut == umax})};
    else
        x0 = {tf == tfopt;
            icollocate({r == xopt1; theta == xopt2; vr == xopt3; vt == xopt4});
            collocate({ur == uopt1; ut == uopt2})};
    end

    % Box constraints
    cbox = {10 <= tf<= tfmax;
        1 <= collocate(r) <= 4;
        0 <= collocate(vr) <= 0.5;
        0 <= collocate(vt) <= 1;
        -umax <= collocate(ur) <= umax;
        -umax <= collocate(ut) <= umax};

    % Boundary constraints
    cbnd = {initial({r == r0; theta == theta0; vr == vr0; vt == vt0})
        final({r == rf; vr == 0; vt == vtf})};

    % ODEs and path constraints
    dr      = vr;
    dtheta  = vt./r;
    dvr     = vt.*vt./r - 1.0./r./r + ur;
    dvt     = -vr.*vt./r + ut;

    ceq = collocate({
        dot(r) == dr;
        dot(theta) == dtheta;
        dot(vr) == dvr;
        dot(vt) == dvt;
        0<=(ur.*ur+ut.*ut).^0.5<=umax});

    % Objective
    objective = integrate((ur.^2+ut.^2).^0.5);

Solve the problem

    options = struct;
    options.name = 'Min Energy Transfer';
    Prob = sym2prob('con',objective, {cbox, cbnd, ceq}, x0, options);
    Prob.KNITRO.options.ALG = 1;
    Prob.KNITRO.options.HONORBNDS = 0;
    Result = tomRun('knitro', Prob, 1);
    solution = getSolution(Result);

    xopt1 = subs(r,solution);
    xopt2 = subs(theta,solution);
    xopt3 = subs(vr,solution);
    xopt4 = subs(vt,solution);
    uopt1 = subs(ur,solution);
    uopt2 = subs(ut,solution);
    tfopt = subs(tf,solution);

===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Min Energy Transfer            f_k       0.523132538752473450
                                       sum(|constr|)      0.000000000014519787
                              f(x_k) + sum(|constr|)      0.523132538766993280
                                              f(x_0)      0.569999999999999170

Solver: KNITRO.  EXIT=0.  INFORM=0.
Interior/Direct NLP KNITRO
Locally optimal solution found

FuncEv   65 GradEv   52 HessEv   52 ConstrEv   64 ConJacEv   52 ConHessEv   51 Iter   51 MinorIter   51
CPU time: 1.578125 sec. Elapsed time: 1.687000 sec. 

===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Min Energy Transfer            f_k       0.523016876584132100
                                       sum(|constr|)      0.000000000094337239
                              f(x_k) + sum(|constr|)      0.523016876678469300
                                              f(x_0)      0.522087806537180010

Solver: KNITRO.  EXIT=0.  INFORM=0.
Interior/Direct NLP KNITRO
Locally optimal solution found

FuncEv   72 GradEv   54 HessEv   54 ConstrEv   71 ConJacEv   54 ConHessEv   53 Iter   53 MinorIter   53
CPU time: 24.062500 sec. Elapsed time: 25.625000 sec. 

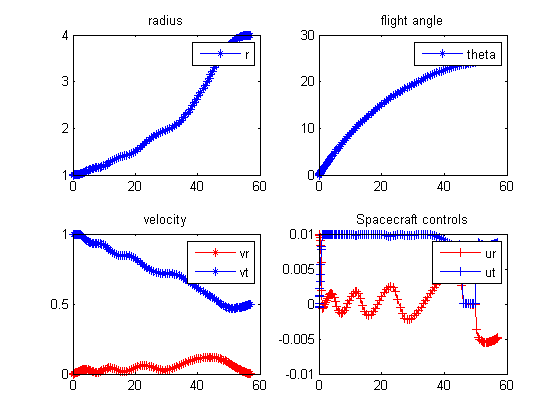
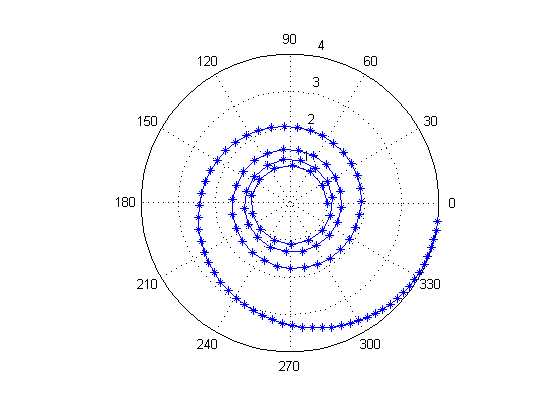
end

% Get final solution
t = subs(icollocate(t),solution);
r = subs(icollocate(r),solution);
theta = subs(icollocate(theta),solution);
vr = subs(icollocate(vr),solution);
vt = subs(icollocate(vt),solution);
ur = subs(icollocate(ur),solution);
ut = subs(icollocate(ut),solution);

t1 = 0:0.5:solution.tf;
r_inter  = interp1p(t,r,t1);
theta_inter  = interp1p(t,theta,t1);
ur_inter = interp1p(t,ur,t1);
ut_inter = interp1p(t,ut,t1);

% Plot final solution
figure(1)
subplot(2,2,1)
plot(t,r,'*-');
legend('r');
title('radius');

subplot(2,2,2)
plot(t,theta,'*-');
legend('theta');
title('flight angle');

subplot(2,2,3)
plot(t,vr,'r*-',t,vt,'b*-');
legend('vr','vt');
title('velocity');

subplot(2,2,4)
plot(t,ur,'r+-',t,ut,'b+-');
legend('ur','ut');
title('Spacecraft controls');

figure(2)
polar(theta_inter,r_inter,'*-')
grid on
axis equal