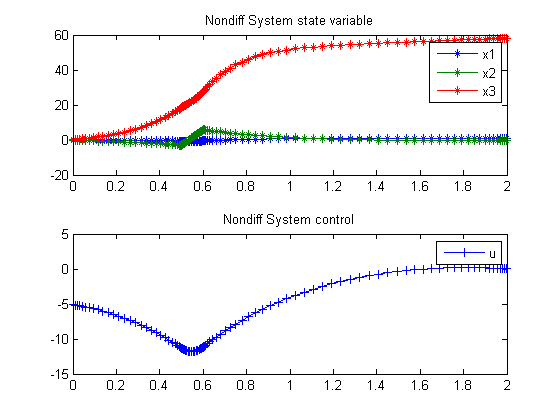
Nondifferentiable system
Global Optimization of Chemical Processes using Stochastic Algorithms 1996, Julio R. Banga, Warren D. Seider
Case Study IV: Optimal control of a nondifferentiable system
Contents
Problem description
This problem has been studied by Thomopoulos and Papadakis who report convergence difficulties using several optimization algorithms and by Luus using Iterative Dynamic Programming. The optimal control problem is:
Find u(t) to minimize:
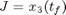
Subject to:
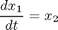
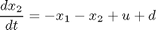
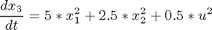
with
![$$ d = 100*[U(t-0.5)-U(t-0.6)] $$](xnondiffSystem_eq93957.png)
where U(t-alpha) is the unit function such that U = 0 for t - alpha < 0 and U = 1 for t - alpha > 0. Hence d is a rectangular pulse of magnitude 100 from t=0.5 until t=0.6. These authors consider tf = 2.0s and the initial conditions:
![$$ x(t_0) = [0 \ 0 \ 0]' $$](xnondiffSystem_eq54671.png)
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
toms t1 p1 = tomPhase('p1', t1, 0, 0.5, 30); toms t2 p2 = tomPhase('p2', t2, 0.5, 0.1, 20); toms t3 p3 = tomPhase('p3', t3, 0.6, 2-0.6, 50); x1p1 = tomState(p1,'x1p1'); x2p1 = tomState(p1,'x2p1'); x3p1 = tomState(p1,'x3p1'); up1 = tomControl(p1,'up1'); x1p2 = tomState(p2,'x1p2'); x2p2 = tomState(p2,'x2p2'); x3p2 = tomState(p2,'x3p2'); up2 = tomControl(p2,'up2'); x1p3 = tomState(p3,'x1p3'); x2p3 = tomState(p3,'x2p3'); x3p3 = tomState(p3,'x3p3'); up3 = tomControl(p3,'up3'); % Initial guess x0 = {icollocate(p1,{x1p1 == 0;x2p1 == 0;x3p1 == 0}) icollocate(p2,{x1p2 == 0;x2p2 == 0;x3p2 == 0}) icollocate(p3,{x1p3 == 0;x2p3 == 0;x3p3 == 0}) collocate(p1,up1==-4-8*t1/0.5) collocate(p2,up2==-12) collocate(p3,up3==-12+14*t3/2)}; % Box constraints cbox = { icollocate(p1,{-100 <= x1p1 <= 100 -100 <= x2p1 <= 100 -100 <= x3p1 <= 100}) icollocate(p2,{-100 <= x1p2 <= 100 -100 <= x2p2 <= 100 -100 <= x3p2 <= 100}) icollocate(p3,{-100 <= x1p3 <= 100 -100 <= x2p3 <= 100 -100 <= x3p3 <= 100}) collocate(p1,-15 <= up1 <= 2) collocate(p2,-15 <= up2 <= 2) collocate(p3,-15 <= up3 <= 2)}; % Boundary constraints cbnd = {initial(p1,{x1p1 == 0;x2p1 == 0;x3p1 == 0}) final(p3,x3p3) <= 60}; % ODEs and path constraints ceq = {collocate(p1,{ dot(p1,x1p1) == x2p1 dot(p1,x2p1) == -x1p1-x2p1+up1 dot(p1,x3p1) == 5*x1p1.^2+2.5*x2p1.^2+0.5*up1.^2}) collocate(p2,{ dot(p2,x1p2) == x2p2 dot(p2,x2p2) == -x1p2-x2p2+up2+100 dot(p2,x3p2) == 5*x1p2.^2+2.5*x2p2.^2+0.5*up2.^2}) collocate(p3,{ dot(p3,x1p3) == x2p3 dot(p3,x2p3) == -x1p3-x2p3+up3 dot(p3,x3p3) == 5*x1p3.^2+2.5*x2p3.^2+0.5*up3.^2})}; % Objective objective = final(p3,x3p3); % Link phase link = {final(p1,x1p1) == initial(p2,x1p2) final(p1,x2p1) == initial(p2,x2p2) final(p1,x3p1) == initial(p2,x3p2) final(p2,x1p2) == initial(p3,x1p3) final(p2,x2p2) == initial(p3,x2p3) final(p2,x3p2) == initial(p3,x3p3)};
Solve the problem
options = struct;
options.name = 'Nondiff System';
constr = {cbox, cbnd, ceq, link};
solution = ezsolve(objective, constr, x0, options);
t = subs(collocate(p1,t1),solution);
t = [t;subs(collocate(p2,t2),solution)];
t = [t;subs(collocate(p3,t3),solution)];
x1 = subs(collocate(p1,x1p1),solution);
x1 = [x1;subs(collocate(p2,x1p2),solution)];
x1 = [x1;subs(collocate(p3,x1p3),solution)];
x2 = subs(collocate(p1,x2p1),solution);
x2 = [x2;subs(collocate(p2,x2p2),solution)];
x2 = [x2;subs(collocate(p3,x2p3),solution)];
x3 = subs(collocate(p1,x3p1),solution);
x3 = [x3;subs(collocate(p2,x3p2),solution)];
x3 = [x3;subs(collocate(p3,x3p3),solution)];
u = subs(collocate(p1,up1),solution);
u = [u;subs(collocate(p2,up2),solution)];
u = [u;subs(collocate(p3,up3),solution)];
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Nondiff System f_k 58.065029206274886000
sum(|constr|) 0.000060625722924220
f(x_k) + sum(|constr|) 58.065089831997810000
f(x_0) 0.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 44 ConJacEv 44 Iter 37 MinorIter 1182
CPU time: 1.390625 sec. Elapsed time: 1.453000 sec.
Plot result
subplot(2,1,1) plot(t,x1,'*-',t,x2,'*-',t,x3,'*-'); legend('x1','x2','x3'); title('Nondiff System state variable'); subplot(2,1,2) plot(t,u,'+-'); legend('u'); title('Nondiff System control');