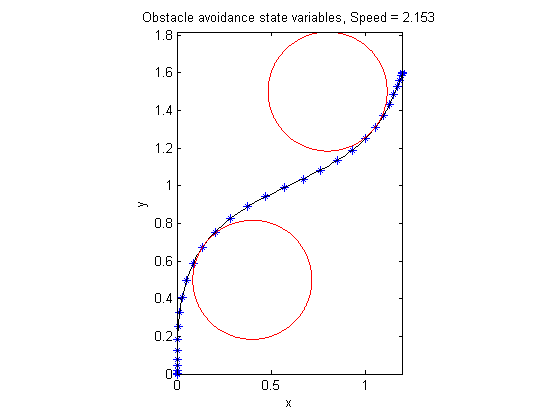
Obstacle Avoidance

OPTRAGEN 1.0 A MATLAB Toolbox for Optimal Trajectory Generation, Raktim Bhattacharya, Texas A&M University (Note: There is typographical error in the OPTRAGEN documentation. The objective involves second derivatives of x and y.)

A robot with obstacles in 2D space. Travel from point A to B using minimum energy.

Contents

Problem Formulation

Find theta(t) and V over t in [0; 1 ] to minimize

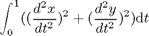
$$ \int_0^{1} ( (\frac{d^2x}{dt^2})^2 + (\frac{d^2y}{dt^2})^2 ) \mathrm{d}t $$

subject to:

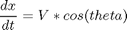
$$ \frac{dx}{dt} = V*cos(theta) $$

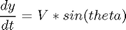
$$ \frac{dy}{dt} = V*sin(theta) $$

$$ [x_0 \ y_0] = [0 \ 0] $$

$$ [x_1 \ y_1] = [1.2 \ 1.6] $$

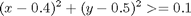
$$ (x-0.4)^2 + (y-0.5)^2 >= 0.1 $$

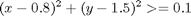
$$ (x-0.8)^2 + (y-1.5)^2 >= 0.1 $$

Where V is a constant scalar speed.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

clear pi % 3.14159... unless someone has set it to something else!

toms t V

tf = 1; % final time

% Starting guess
speed = 5;
xopt = 1.2*t;
yopt = 1.6*t;
vxopt = 1.2;
vyopt = 1.6;
thetaopt = pi/4;

Solve the problem, using a successively larger number collocation points

for n=[4 15 30]

    % Create a new phase and states, using n collocation points
    p = tomPhase('p', t, 0, tf, n);
    setPhase(p);
    tomStates x y vx vy
    tomControls theta

    % Interpolate an initial guess for the n collocation points
    x0 = {V == speed
        icollocate({x == xopt; y == yopt; vx == vxopt; vy == vyopt})
        collocate(theta == thetaopt)};

    % Box constraints
    cbox = {0 <= V <= 100 };

    % Boundary constraints
    cbnd = {initial({x == 0; y == 0})
        final({x == 1.2; y == 1.6})};

    % ODEs and path constraints
    ode = collocate({
        dot(x) == vx == V*cos(theta)
        dot(y) == vy == V*sin(theta)
        });

    % A 30th order polynomial is more than sufficient to give good
    % accuracy. However, that means that mcollocate would only check
    % about 60 points. In order to make sure we don't hit an obstacle,
    % we check 300 evenly spaced points instead, using atPoints.
    obstacles = atPoints(linspace(0,tf,300), {
        (x-0.4)^2 + (y-0.5)^2 >= 0.1
        (x-0.8)^2 + (y-1.5)^2 >= 0.1});

    % Objective: minimum energy.
    objective = integrate(dot(vx)^2+dot(vy)^2);

Solve the problem

    options = struct;
    options.name = 'Obstacle avoidance';
    constr = {cbox, cbnd, ode, obstacles};
    solution = ezsolve(objective, constr, x0, options);

    % Optimal x, y, and speed, to use as starting guess in the next iteration
    xopt = subs(x, solution);
    yopt = subs(y, solution);
    vxopt = subs(vx, solution);
    vyopt = subs(vy, solution);
    thetaopt = subs(theta, solution);
    speed = subs(V,solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Obstacle avoidance             f_k      29.812856165009947000
                                       sum(|constr|)      0.000000001309307815
                              f(x_k) + sum(|constr|)     29.812856166319254000
                                              f(x_0)      0.000000000000062528

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   22 ConJacEv   22 Iter   20 MinorIter 2732
CPU time: 0.625000 sec. Elapsed time: 0.672000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Obstacle avoidance             f_k      22.128728366249842000
                                       sum(|constr|)      0.000000000006805542
                              f(x_k) + sum(|constr|)     22.128728366256649000
                                              f(x_0)     29.812856165009237000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  151 ConJacEv  151 Iter  136 MinorIter  480
CPU time: 2.296875 sec. Elapsed time: 2.344000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Obstacle avoidance             f_k      22.091923326555573000
                                       sum(|constr|)      0.000000000010556925
                              f(x_k) + sum(|constr|)     22.091923326566132000
                                              f(x_0)     22.128728366252837000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  322 ConJacEv  322 Iter  293 MinorIter  697
CPU time: 9.671875 sec. Elapsed time: 9.734000 sec. 

end

Plot result

figure(1)
th = linspace(0,2*pi,500);
x1 = sqrt(0.1)*cos(th)+0.4;
y1 = sqrt(0.1)*sin(th)+0.5;
x2 = sqrt(0.1)*cos(th)+0.8;
y2 = sqrt(0.1)*sin(th)+1.5;
ezplot(x,y);
hold on
plot(x1,y1,'r',x2,y2,'r');
hold off
xlabel('x');
ylabel('y');
title(sprintf('Obstacle avoidance state variables, Speed = %2.4g',speed));
axis image