Oil Shale Pyrolysis
Dynamic Optimization of Batch Reactors Using Adaptive Stochastic Algorithms 1997, Eugenio F. Carrasco, Julio R. Banga
Case Study II: Oil Shale Pyrolysis
Contents
Problem description
A very challenging optimal control problem is the oil shale pyrolysis case study, as considered by Luus (1994). The system consists of a series of five chemical reactions:
A1 -> A2
A2 -> A3
A1+A2 -> A2+A2
A1+A2 -> A3+A2
A1+A2 -> A4+A2
This system is described by the differential equations
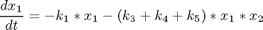
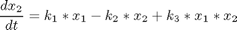
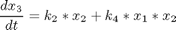
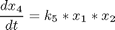
where the state variables are the concentrations of species, Ai, i = 1, ..., 4. The initial condition is
![$$ x(t_0) = [1 \ 0 \ 0 \ 0]' $$](xoilPyrolysis_eq78251.png)
The rate expressions are given by:
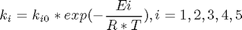
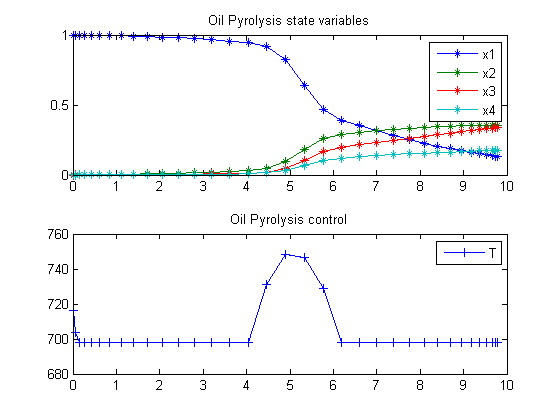
where the values of ki0 and Ei are given by Luus (1994). The optimal control problem is to find the residence time tf and the temperature profile T(t) in the time interval 0 <= t <= tf so that the production of pyrolytic bitumen, given by x2, is maximized. Therefore, the performance index is
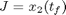
The constraints on the control variable (temperature) are:
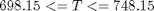
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
toms t toms tf ai = [8.86; 24.25; 23.67; 18.75; 20.70]; bi = [20300; 37400; 33800; 28200; 31000]/1.9872; for n=[4 10 20 30 35]
p = tomPhase('p', t, 0, tf, n); setPhase(p); tomStates x1 x2 x3 x4 tomControls T % Initial guess if n == 4 x0 = {tf == 9.3 collocate(T == 725)}; else x0 = {tf == tfopt icollocate({ x1 == x1opt; x2 == x2opt x3 == x3opt; x4 == x4opt }) collocate(T == Topt)}; end % Box constraints cbox = {9.1 <= tf <= 12 icollocate({0 <= x1 <= 1; 0 <= x2 <= 1 0 <= x3 <= 1; 0 <= x4 <= 1}) 698.15 <= collocate(T) <= 748.15}; % Boundary constraints cbnd = initial({x1 == 1; x2 == 0; x3 == 0; x4 == 0}); % ODEs and path constraints ki1 = exp(ai(1)-bi(1)./T); ki2 = exp(ai(2)-bi(2)./T); ki3 = exp(ai(3)-bi(3)./T); ki4 = exp(ai(4)-bi(4)./T); ki5 = exp(ai(5)-bi(5)./T); ceq = collocate({ dot(x1) == -ki1.*x1-(ki3+ki4+ki5).*x1.*x2 dot(x2) == ki1.*x1-ki2.*x2+ki3.*x1.*x2 dot(x3) == ki2.*x2+ki4.*x1.*x2 dot(x4) == ki5.*x1.*x2}); % Objective objective = -final(x2);
Solve the problem
options = struct;
options.name = 'Oil Pyrolysis';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
x1opt = subs(x1, solution);
x2opt = subs(x2, solution);
x3opt = subs(x3, solution);
x4opt = subs(x4, solution);
Topt = subs(T, solution);
tfopt = subs(final(t), solution);
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Oil Pyrolysis f_k -0.357327805323273680
sum(|constr|) 0.000000000957533264
f(x_k) + sum(|constr|) -0.357327804365740410
f(x_0) 0.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 93 ConJacEv 93 Iter 50 MinorIter 193
CPU time: 0.203125 sec. Elapsed time: 0.203000 sec.
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Oil Pyrolysis f_k -0.352623357520822740
sum(|constr|) 0.000000551130763617
f(x_k) + sum(|constr|) -0.352622806390059110
f(x_0) -0.357327805323273680
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 181 ConJacEv 181 Iter 105 MinorIter 260
CPU time: 0.453125 sec. Elapsed time: 0.453000 sec.
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Oil Pyrolysis f_k -0.353724616475626360
sum(|constr|) 0.000000011438338683
f(x_k) + sum(|constr|) -0.353724605037287700
f(x_0) -0.352623357520823520
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 100 ConJacEv 100 Iter 75 MinorIter 239
CPU time: 0.390625 sec. Elapsed time: 0.391000 sec.
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Oil Pyrolysis f_k -0.353702100040879430
sum(|constr|) 0.000000010781458740
f(x_k) + sum(|constr|) -0.353702089259420700
f(x_0) -0.353724616475625140
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 138 ConJacEv 138 Iter 64 MinorIter 336
CPU time: 0.750000 sec. Elapsed time: 0.781000 sec.
Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Oil Pyrolysis f_k -0.353537539518337880
sum(|constr|) 0.000058025124637268
f(x_k) + sum(|constr|) -0.353479514393700620
f(x_0) -0.353702100040879320
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 51 ConJacEv 51 Iter 43 MinorIter 285
CPU time: 0.468750 sec. Elapsed time: 0.516000 sec.
end
t = subs(collocate(t),solution);
x1 = subs(collocate(x1opt),solution);
x2 = subs(collocate(x2opt),solution);
x3 = subs(collocate(x3opt),solution);
x4 = subs(collocate(x4opt),solution);
T = subs(collocate(Topt),solution);
Plot result
subplot(2,1,1) plot(t,x1,'*-',t,x2,'*-',t,x3,'*-',t,x4,'*-'); legend('x1','x2','x3','x4'); title('Oil Pyrolysis state variables'); subplot(2,1,2) plot(t,T,'+-'); legend('T'); title('Oil Pyrolysis control');