Parametric Sensitivity Control

Optimal Parametric Sensitivity control of a fed-batch reactor

Contents

Problem description

From the paper: J.D. Stigter, K.J. Keesman, 2004, "Optimal Parametric Sensitivity control of a fed-batch reactor", Automatica, 40, 4, pp. 1459-1464.

Programmer: Gerard Van Willigenburg (Wageningen University)

% Copyright (c) 2009-2009 by Tomlab Optimization Inc.

Problem setup

toms t

tf = 250; % Fixed final time
p = tomPhase('p', t, 0, tf, 25);
setPhase(p)

tomStates x1 x2 x3 x4
tomControls u

% Initial state amd maximum control
xi   = [0; 0; 0; 0];
umax = 20;
x    = [x1; x2; x3; x4];

% Initial guess
x0 = {icollocate(x == xi)
    collocate(u == umax)};

% Box constraints
cbox = {collocate({0 <= u <= umax; 0 <= x1 <= 100})};

% Boundary constraints
cbnd = initial(x == xi);

% Bio kinectic parameters
mu_m = 2.62e-4; Y = 0.64; K_S = 1.0;
X    = 4e3; muXY = mu_m*X/Y;

% Sensitivity parameters
q = [1 3e-2]/250;

% Odes: state and state sensitivity dynamics
Kx1 = K_S+x1; Kx12 = Kx1*Kx1;

ceq = collocate({
    dot(x1) == -muXY*x1/Kx1 + u
    dot(x2) == muXY*(x1-K_S*x2)/Kx12
    dot(x3) == -muXY*K_S*x3/Kx12-x1/Kx1
    dot(x4) == q(1)*x2*x2+q(2)*x3*x3});

% Objective
objective = -final(x4);

Solve the problem

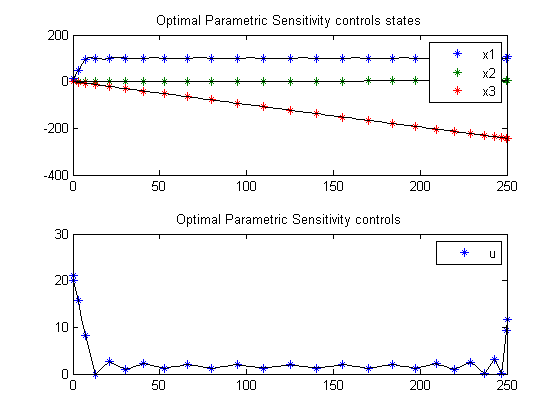
options = struct;
options.name = 'Optimal Parametric Sensitivity';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

% Plot intermediate results
subplot(2,1,1);
ezplot([x1; x2; x3]); legend('x1','x2','x3');
title('Optimal Parametric Sensitivity controls states');

subplot(2,1,2);
ezplot(u); legend('u');
title('Optimal Parametric Sensitivity controls'); drawnow;

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Optimal Parametric Sensitivity  f_k    -599.557785475654670000
                                        sum(|constr|)      0.000004222520124963
                               f(x_k) + sum(|constr|)   -599.557781253134520000
                                               f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  251 ConJacEv  251 Iter  126 MinorIter 1415
CPU time: 0.796875 sec. Elapsed time: 0.797000 sec.