Orbit Raising Minimum Time

Contents

Problem description

Minimize:

$$ J = t_f $$

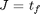
subject to the dynamic constraints

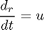
$$ \frac{d_r}{dt} = u $$

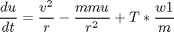
$$ \frac{du}{dt} = \frac{v^2}{r}-\frac{mmu}{r^2}+T*\frac{w1}{m} $$

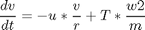
$$ \frac{dv}{dt} = -u*\frac{v}{r}+T*\frac{w2}{m} $$

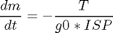
$$ \frac{dm}{dt} = -\frac{T}{g0*ISP} $$

the boundary conditions

$$ r(t_0) = 1 $$

$$ u(t_0) = 1 $$

$$ u(t_f) = 0 $$

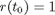
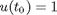
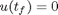
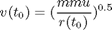
$$ v(t_0) = (\frac{mmu}{r(t_0)})^{0.5} $$

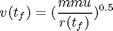
$$ v(t_f) = (\frac{mmu}{r(t_f)})^{0.5} $$

$$ m(t_0) = 1 $$

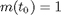
where w1 = sin(phi) and w2 = cos(phi)

At t_f, r and m are free.

% Copyright (c) 2007-2009 by Tomlab Optimization Inc.

Problem setup

mmu     = 1;
t_f    = 3.32;  m_0    = 1;            r_0    = 1;   u_0    = 0;
u_f    = 0;     v_0    = sqrt(mmu/r_0); rmin   = 0.9; rmax   = 5;
umin   = -5;    umax   = 5;            vmin   = -5;  vmax   = 5;
mmax   = m_0;   mmin   = 0.1;          tf_min = 0.5; tf_max = 10;
r_f     = 1.5;

T  = 0.1405;
Ve = 1.8758;

toms t t_f
p1 = tomPhase('p1', t, 0, t_f, 50);
setPhase(p1);

tomStates r u v m

% The problem becomes less nonlinear if w1 and w2 are control variables
% (with the constraints w1^2+w2^2==1) than if phi is the control varialbe
% (with w1 and w2 being nonlinear functions of phi).
tomControls w1 w2
phi = atan2(w1,w2);

% Initial guess
x0 = {t_f == 3.32
    icollocate({
    r == r_0+(r_f-r_0)*t/t_f
    u == 0.1
    v == v_0
    m == m_0-(T/Ve)*t})
    collocate({
    w1 == -0.7*sign(t-t_f/2)
    w2 == 0.4
    })};

% Boundary constraints
cbnd = {initial({
    r == r_0
    u == u_0
    v == v_0
    m == m_0
    })
    final({
    r == r_f
    u == u_f
    v == sqrt(mmu/r)})};

% Box constraints
cbox = {0.5 <= t_f <= 10
    rmin <= icollocate(r) <= rmax
    umin <= icollocate(u) <= umax
    vmin <= icollocate(v) <= vmax
    };

% ODEs and path constraints
ceq = collocate({
    dot(r) == u
    dot(u) == v^2/r-mmu/r^2+T*w1/m
    dot(v) == -u*v/r+T*w2/m
    dot(m) == -T/Ve
    w1^2+w2^2 == 1
    });

% Objective
objective = t_f;

Solve the problem

options = struct;
options.name = 'Orbit Raising Problem Min Time';
options.scale = 'manual'; % Auto-scaling is not really needed as all variables are already reasonably scaled.
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

Problem type appears to be: lpcon
Warning: Initial guess out of bounds for the variable u_p1 
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2011-02-05
=====================================================================================
Problem: ---  1: Orbit Raising Problem Min Time  f_k       3.248079535630944200
                                        sum(|constr|)      0.000032253415551923
                               f(x_k) + sum(|constr|)      3.248111789046496300
                                               f(x_0)      3.319999999999999800

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   68 ConJacEv   68 Iter   35 MinorIter  283
CPU time: 1.937500 sec. Elapsed time: 1.125000 sec.

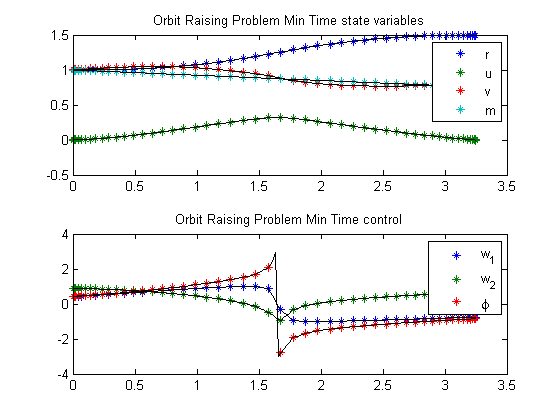
Plot result

subplot(2,1,1)
ezplot([r u v m]);
legend('r','u','v','m');
title('Orbit Raising Problem Min Time state variables');

subplot(2,1,2)
ezplot([w1 w2 phi])
legend('w_1', 'w_2', '\phi');
title('Orbit Raising Problem Min Time control');