Park-Ramirez bioreactor
Dynamic optimization of chemical and biochemical processes using restricted second-order information 2001, Eva Balsa-Canto, Julio R. Banga, Antonio A. Alonso Vassilios S. Vassiliadis
Case Study I: Park-Ramirez bioreactor
Contents
Problem description
This case study deals with the optimal production of secreted protein in a fed-batch reactor. It was originally formulated by Park and Ramirez (Park & Ramirez, 1988) and it has also been considered by other researchers (Vassiliadis, 1993; Yang & Wu, 1994; Banga, Irizarry & Seider, 1995; Luus, 1995; Tholudur & Ramirez, 1997). The objective is to maximize the secreted heterologous protein by a yeast strain in a fed-batch culture. The dynamic model accounts for host-cell growth, gene expression, and the secretion of expressed polypeptides. The mathematical statement is as follows:
Find u(t) over t in [t0,tf] to maximize:
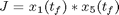
subject to:
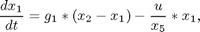
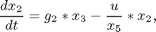
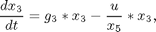
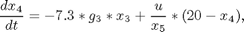
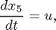
with:
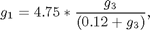
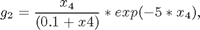
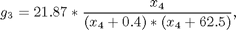
where x1 and x2 are, respectively, the concentration of the secreted protein and the total protein (l-1), x3 is the culture cell density (g l-1), x4 is the substrate concentration (g l-1), x5 is the holdup volume (l), u is the nutrient (glucose) feed rate (l h-1), and J is the mass of protein produced (in arbitrary units). The initial conditions are:
![$$ x(t_0) = [0 \ 0 \ 1 \ 5 \ 1]' $$](xparkBioReactor_eq37175.png)
For final time tf = 15 h, and the following constraints on the control variable:

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
toms t
Solve the problem, using a successively larger number collocation points
for n=[20 40 80 120]
p = tomPhase('p', t, 0, 15, n); setPhase(p); tomStates z1 z2 z3 z4 z5 tomControls u if n>20 % Interpolate an initial guess for the n collocation points x0 = {icollocate({z1 == z1opt; z2 == z2opt z3 == z3opt; z4 == z4opt; z5 == z5opt}) collocate(u == uopt)}; else x0 = {}; end % Box constraints cbox = {icollocate({z1 <= 3 z2 <= 3; 0 <= z3 <= 4 0 <= z4 <= 10; 0.5 <= z5 <= 25}) 0 <= collocate(u) <= 2.5}; % Boundary constraints cbnd = initial({z1 == 0; z2 == 0; z3 == 1 z4 == 5; z5 == 1}); % Various constants and expressions g3 = 21.87*z4./(z4+.4)./(z4+62.5); g1 = 4.75*g3./(0.12+g3); g2 = z4./(0.1+z4).*exp(-5*z4); % ODEs and path constraints ceq = collocate({ dot(z1) == g1.*(z2-z1)-u./z5.*z1 dot(z2) == g2.*z3-u./z5.*z2 dot(z3) == g3.*z3-u./z5.*z3 dot(z4) == -7.3*g3.*z3+u./z5.*(20-z4) dot(z5) == u}); % Secreted protein must be less than total protein % proteinlimit = {z1 <= z2}; % Objective if n == 120 objective = -final(z1)*final(z5)+var(diff(collocate(u))); else objective = -final(z1)*final(z5); end
Solve the problem
options = struct;
options.name = 'Park Bio Reactor';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
% Optimal z and u, to use as starting guess in the
% next iteration
z1opt = subs(z1, solution);
z2opt = subs(z2, solution);
z3opt = subs(z3, solution);
z4opt = subs(z4, solution);
z5opt = subs(z5, solution);
uopt = subs(u, solution);
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Park Bio Reactor f_k -35.421698724161942000
sum(|constr|) 0.000000000990670617
f(x_k) + sum(|constr|) -35.421698723171275000
f(x_0) 0.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 134 ConJacEv 134 Iter 100 MinorIter 814
CPU time: 0.656250 sec. Elapsed time: 0.657000 sec.
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Park Bio Reactor f_k -33.571631159656995000
sum(|constr|) 0.000000000128376368
f(x_k) + sum(|constr|) -33.571631159528621000
f(x_0) -35.421698724161729000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 115 ConJacEv 115 Iter 101 MinorIter 504
CPU time: 1.703125 sec. Elapsed time: 1.719000 sec.
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Park Bio Reactor f_k -33.154158230075637000
sum(|constr|) 0.000000000115840908
f(x_k) + sum(|constr|) -33.154158229959798000
f(x_0) -33.571631159657159000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 189 ConJacEv 189 Iter 186 MinorIter 704
CPU time: 15.531250 sec. Elapsed time: 15.594000 sec.
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Park Bio Reactor f_k -32.718180228309564000
sum(|constr|) 0.000000004625834596
f(x_k) + sum(|constr|) -32.718180223683731000
f(x_0) -32.743854320903381000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 154 ConJacEv 154 Iter 139 MinorIter 866
CPU time: 45.765625 sec. Elapsed time: 46.656000 sec.
end
t = subs(collocate(t),solution);
z1 = collocate(z1opt);
z2 = collocate(z2opt);
z3 = collocate(z3opt);
z4 = collocate(z4opt);
z5 = collocate(z5opt);
u = collocate(uopt);
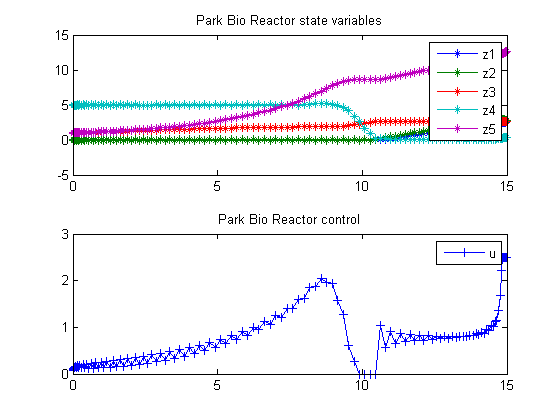
Plot result
subplot(2,1,1) plot(t,z1,'*-',t,z2,'*-',t,z3,'*-',t,z4,'*-',t,z5,'*-'); legend('z1','z2','z3','z4','z5'); title('Park Bio Reactor state variables'); subplot(2,1,2) plot(t,u,'+-'); legend('u'); title('Park Bio Reactor control');