Pendulum Gravity Estimation

User's Guide for DIRCOL

Problem 2.5 Pendulum

Contents

Problem Formulation

Find u over t in [0; 2 ] to minimize

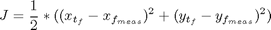
$$ J = \frac{1}{2}*((x_{t_f}-x_{f_{meas}})^2 + (y_{t_f}-y_{f_{meas}})^2) $$

subject to:

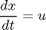
$$ \frac{dx}{dt} = u $$

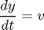
$$ \frac{dy}{dt} = v $$

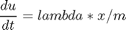
$$ \frac{du}{dt} = lambda*x/m $$

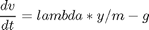
$$ \frac{dv}{dt} = lambda*y/m-g $$

$$ x^2 + y^2 - L^2 = 0 $$

$$ [x_0 \ y_0 \ u_0 \ v_0] = [0.4 \ -0.3 \ 0 \ 0] $$

$$ [x_{f_{meas}} \ y_{f_{meas}}] = [-0.231625 \ -0.443109] $$

$$ L = 0.5 $$

$$ m = 0.3 $$

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t g

% Initial guess
gopt = 20;
xopt = 0.4-(0.4+0.231625)*t/2;
yopt = -0.3-(-0.3+0.443109)*t/2;
uopt = 0;
vopt = 0;
lambdaopt = -5;

for n=[20 51]

    p = tomPhase('p', t, 0, 2, n);
    setPhase(p);
    tomStates x y u v
    tomControls lambda

    % Initial guess
    x0 = {g == gopt
        icollocate({
        x == xopt
        y == yopt
        u == uopt
        v == vopt})
        collocate(lambda == lambdaopt)};

    % Box constraints
    cbox = {1 <= g <= 100};

    % Boundary constraints
    cbnd = initial({x == 0.4; y == -0.3
        u == 0; v == 0});

    L   = 0.5;
    m   = 0.3;
    xmeas = -0.231625;
    ymeas = -0.443109;

    % ODEs and path constraints
    ceq = collocate({
        dot(x) == u
        dot(y) == v
        dot(u) == lambda.*x/m
        dot(v) == lambda.*y/m-g
        x.^2 + y.^2 - L^2 == 0});

    % Objective
    objective = 1/2*((final(x)-xmeas)^2+(final(y)-ymeas)^2);

Solve the problem

    options = struct;
    options.name = 'Pendulum Gravity';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
    gopt = subs(g, solution);
    xopt = subs(x, solution);
    yopt = subs(y, solution);
    uopt = subs(u, solution);
    vopt = subs(v, solution);
    lambdaopt = subs(lambda, solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Pendulum Gravity               f_k       0.000000017178910877
                                       sum(|constr|)      0.000000782774920603
                              f(x_k) + sum(|constr|)      0.000000799953831480
                                              f(x_0)     -0.124997863253000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  110 ConJacEv  110 Iter   45 MinorIter   91
CPU time: 0.250000 sec. Elapsed time: 0.250000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Pendulum Gravity               f_k       0.000000000014570095
                                       sum(|constr|)      0.000000123532555605
                              f(x_k) + sum(|constr|)      0.000000123547125700
                                              f(x_0)     -0.124997846074089260

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    7 ConJacEv    7 Iter    6 MinorIter  132
CPU time: 0.250000 sec. Elapsed time: 0.250000 sec. 

end

Show result

disp(sprintf('Gravity estimated to %g',gopt));

Gravity estimated to 9.82655