Penicillin Plant
Fed-batch Fermentor Control: Dynamic Optimization of Batch Processes II. Role of Measurements in Handling Uncertainty 2001, B. Srinivasan, D. Bonvin, E. Visser, S. Palanki
Illustrative example: Nominal Optimization of a Fed-Batch Fermentor for Penicillin Production.
Contents
Problem description
This particular example was featured in the work of B. Srinivasan et al. 2001. The optimal trajectories for the problem was provided in the work.
In this problem, the objective is to maximize the concentration of penicillin, P, produced in a fed-batch bioreactor, given a finite amount of time.
Reactions: S -> X, S -> P Conditions: Fed-batch, isothermal. Objective: Maximize the concentration of product P at a given final time. Manipulated variable: Feed rate of S. Constraints: Input bounds; upper limit on the biomass concentration, which is motivated by oxygen-transfer limitation typically occurring at large biomass concentration.
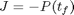
subject to:
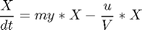
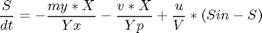
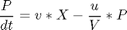
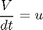
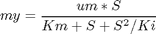
Programmer: Wee Kiat Lim (Nanyang Technological University)
% Copyright (c) 2009-2009 by Tomlab Optimization Inc.
Problem setup
Penalty for variations in u
penalty_constant = 0.001; % Various constants miu_m = 0.02; Km = 0.05; Ki = 5; Yx = 0.5; Yp = 1.2; v = 0.004; Sin = 200; umin = 0; umax = 1; Xmin = 0; Xmax = 3.7; Smin = 0; % no. of collocation points to use narr = [30 100]; for n=narr toms t1 toms tcut p1 = tomPhase('p1', t1, 0, tcut, n); setPhase(p1); tomStates X1 S1 P1 V1 %Vs %Scaling is disabled here tomControls u1 % Initial guess if n == narr(1) x01 = {tcut == 75 icollocate({X1 == 1+2.7*t1/tcut; S1 == 0.5; P1 == 0.6*t1/tcut; V1 == 150}) collocate(u1 == 0.03+0.06*t1/tcut)}; else x01 = {tcut == tcutg icollocate({X1 == Xg1; S1 == Sg1; P1 == Pg1; V1 == Vg1}) collocate(u1 == ug1)}; end % Box constraints cbox1 = {75 <= tcut <= 85 0 <= icollocate(X1) <= Xmax Smin <= icollocate(S1) <= 100 0 <= icollocate(P1) <= 5 1 <= icollocate(V1) <= 300 umin <= collocate(u1) <= umax}; % Boundary constraints cbnd1 = initial({X1 == 1; S1 == 0.5; P1 == 0; V1 == 150}); miu1 = (miu_m*S1)/(Km + S1 + S1^2/Ki); % ODEs and path constraints temp11 = miu1*X1; temp21 = u1/V1; temp31 = v*X1; ceq1 = collocate ({ dot(X1) == temp11 - u1/V1*X1 dot(S1) == -temp11/Yx - temp31/Yp + temp21*(Sin - S1) dot(P1) == temp31 - temp21*P1 dot(V1) == u1}); if n == narr(1) % No objective in first phase objective = 0; else % Variation penalty objective = penalty_constant*integrate(dot(u1)^2); end toms t2 p2 = tomPhase('p2', t2, tcut, 150-tcut, n); setPhase(p2); tomStates X2 S2 P2 V2 %Vs %Scaling is disabled here tomControls u2 % Initial guess if n == narr(1) x02 = {icollocate({X2 == Xmax; S2 == 0; P2 == 0.6+t2/150; V2 == 150}); collocate(u2 == 0.01)}; else x02 = {icollocate({X2 == Xg2; S2 == Sg2; P2 == Pg2; V2 == Vg2}) collocate(u2 == ug2)}; end % Box constraints umax2 = 0.03; cbox2 = {0 <= icollocate(X2) <= Xmax Smin <= icollocate(S2) <= 100 0 <= icollocate(P2) <= 5 1 <= icollocate(V2) <= 300 umin <= collocate(u2) <= umax2 initial(S2) <= 0.2}; miu2 = (miu_m*S2)/(Km + S2 + S2^2/Ki); % ODEs and path constraints temp12 = miu2*X2; temp22 = u2/V2; temp32 = v*X2; ceq2 = collocate ({ dot(X2) == temp12 - u2/V2*X2 dot(S2) == -temp12/Yx - temp32/Yp + temp22*(Sin - S2) dot(P2) == temp32 - temp22*P2 dot(V2) == u2}); % Phase links links = {initial(X2) == final(p1,X1) initial(S2) == final(p1,S1) initial(P2) == final(p1,P1) initial(V2) == final(p1,V1)}; if n == narr(1) % Objective (Negative sign is added to 'maximize' P) objective = -final(P2); type = 'lpcon'; solver = 'snopt'; else objective = objective-final(P2)+penalty_constant*integrate(dot(u2)^2); type = 'con'; solver = 'snopt'; end % Solve the problem options = struct; options.name = 'Penicillin Plant'; Prob = sym2prob(type, objective, {cbox1, cbnd1, ceq1, cbox2, ceq2, links}, {x01, x02}, options); Result = tomRun(solver, Prob, 1); solution = getSolution(Result); t1 = subs(collocate(p1,t1),solution); t2 = subs(collocate(p2,t2),solution); ug1 = subs(collocate(p1,u1),solution); Xg1 = subs(collocate(p1,X1),solution); Sg1 = subs(collocate(p1,S1),solution); Pg1 = subs(collocate(p1,P1),solution); Vg1 = subs(collocate(p1,V1),solution); ug2 = subs(collocate(p2,u2),solution); Xg2 = subs(collocate(p2,X2),solution); Sg2 = subs(collocate(p2,S2),solution); Pg2 = subs(collocate(p2,P2),solution); Vg2 = subs(collocate(p2,V2),solution); tcutg = solution.tcut; np=length(t1) + length(t2); end
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Penicillin Plant f_k -1.682687588966889100
sum(|constr|) 0.000001056758526911
f(x_k) + sum(|constr|) -1.682686532208362200
f(x_0) -1.600000000000001400
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 126 ConJacEv 126 Iter 68 MinorIter 3734
CPU time: 2.625000 sec. Elapsed time: 2.641000 sec.
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Penicillin Plant f_k -1.682693617368655700
sum(|constr|) 0.000003716816491676
f(x_k) + sum(|constr|) -1.682689900552164100
f(x_0) -1.157798971400167100
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 102 GradEv 100 ConstrEv 100 ConJacEv 100 Iter 60 MinorIter 9857
CPU time: 51.703125 sec. Elapsed time: 53.094000 sec.
Plot result
Optimal states and control trajectories
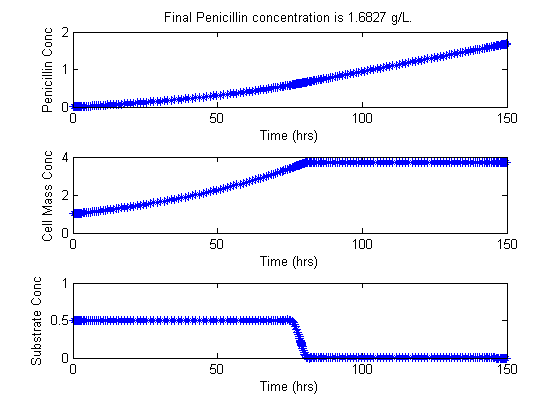
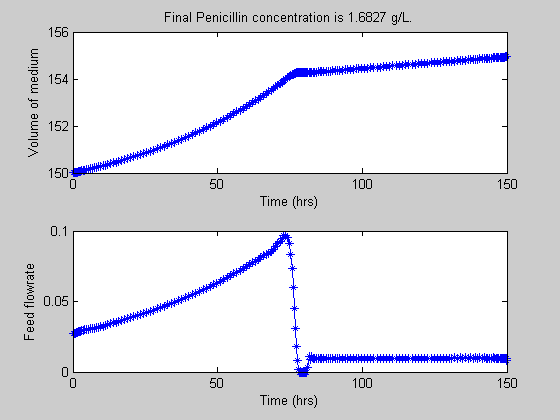
t = [t1;t2]; uopt = [ug1;ug2]; Xopt = [Xg1;Xg2]; Sopt = [Sg1;Sg2]; Popt = [Pg1;Pg2]; Vopt = [Vg1;Vg2]; Pfinal=subs(final(P2),solution); % Plots of the trajectories figure(1) subplot(3,1,1); plot(t,Popt,'*-'); title(['Final Penicillin concentration is ',num2str(Pfinal),' g/L.']) ylabel('Penicillin Conc') xlabel('Time (hrs)') subplot(3,1,2); plot(t,Xopt,'*-'); ylabel('Cell Mass Conc') xlabel('Time (hrs)') subplot(3,1,3); plot(t,Sopt,'*-'); ylabel('Substrate Conc') xlabel('Time (hrs)') figure(2) subplot(2,1,1); plot(t,Vopt,'*-'); title(['Final Penicillin concentration is ',num2str(Pfinal),' g/L.']) ylabel('Volume of medium') xlabel('Time (hrs)') subplot(2,1,2); plot(t,uopt,'*-'); ylabel('Feed flowrate') xlabel('Time (hrs)') fprintf('\n') fprintf('Optimization completed... \n') fprintf('Final Penicillin concentration is %5.4f g/L.\n',Pfinal)
Optimization completed... Final Penicillin concentration is 1.6827 g/L.