Plug-Flow Tubular Reactor

A HYBRID METHOD FOR THE OPTIMAL CONTROL OF CHEMICAL PROCESSES 1998, E F Carrasco, J R Banga

Case Study II: Plug-Flow Tubular Reactor

Contents

Problem description

This case study considers a plug-flow reactor as studied by Reddy and Husain, Luus and Mekarapiruk and Luus. The objective is to maximize the normalized concentration of the desired product.

Find u(t) to maximize

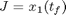
$$ J = x_1(t_f) $$

subject to:

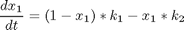
$$ \frac{dx_1}{dt} = (1-x_1)*k_1-x_1*k_2 $$

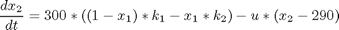
$$ \frac{dx_2}{dt} = 300*((1-x_1)*k_1-x_1*k_2)-u*(x_2-290) $$

where x1 denotes the normalized concentration of de desired product, and x2 is the temperature. The initial conditions are:

$$ x(t_0) = [0 \ 380]' $$

The rate constants are given by:

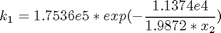
$$ k_1 = 1.7536e5*exp(-\frac{1.1374e4}{1.9872*x_2}) $$

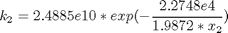
$$ k_2 = 2.4885e10*exp(-\frac{2.2748e4}{1.9872*x_2}) $$

where the final time tf = 5 min. The constraint on the control variable (the normalized coolant flow rate) is:

$$ 0 <= u <= 0.5 $$

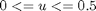
In addition, there is an upper path constraint on the temperature:

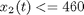
$$ x_2(t) <= 460 $$

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, 0, 5, 30);
setPhase(p);

tomStates x1 x2
tomControls u

% Initial guess
x0 = {icollocate({x1 == 0.6*t/5
    x2 == 380})
    collocate(u == 0.25)};

% Box constraints
cbox = {0 <= icollocate(x1) <= 10
    100 <= icollocate(x2) <= 460
    0   <= collocate(u)   <= 0.5};

% Boundary constraints
cbnd = initial({x1 == 0; x2 == 380});

% ODEs and path constraints
k1 = 1.7536e5*exp(-1.1374e4/1.9872./x2);
k2 = 2.4885e10*exp(-2.2748e4/1.9872./x2);
ceq = collocate({
    dot(x1) == (1-x1).*k1-x1.*k2
    dot(x2) == 300*((1-x1).*k1-x1.*k2)-u.*(x2-290)});

% Objective
objective = -final(x1);

Solve the problem

options = struct;
options.name = 'Plug Flow Reactor';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
t  = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
u  = subs(collocate(u),solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Plug Flow Reactor              f_k      -0.677126028100865080
                                       sum(|constr|)      0.003151412965574960
                              f(x_k) + sum(|constr|)     -0.673974615135290110
                                              f(x_0)     -0.599999999999999200

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv 1287 ConJacEv 1287 Iter  343 MinorIter  514
CPU time: 2.296875 sec. Elapsed time: 2.313000 sec.

Plot result

subplot(2,1,1)
plot(t,x1,'*-',t,x2/100,'*-');
legend('x1','x2/100');
title('Plug Flow Reactor state variables');

subplot(2,1,2)
plot(t,u,'+-');
legend('u');
title('Plug Flow Reactor control');