Quadratic constraint problem

Paper: LINEAR-QUADRATIC OPTIMAL CONTROL WITH INTEGRAL QUADRATIC CONSTRAINTS. OPTIMAL CONTROL APPLICATIONS AND METHODS Optim. Control Appl. Meth., 20, 79-92 (1999)

E. B. LIM(1), Y. Q. LIU(2), K. L. TEO(2) AND J. B. MOORE(1)

(1) Department of Systems Engineering, Research School of Information Sciences and Engineering, Australian National University, Canberra ACT 0200, Australia

(2) School of Mathematics and Statistics, Curtin University of Technology, Perth, WA 6845, Australia

Contents

Problem Formulation

Find u(t) over t in [0; 1 ] to minimize

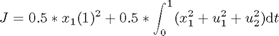
$$ J = 0.5*x_1(1)^2 + 0.5*\int_0^1 (x_1^2 + u_1^2 + u_2^2) \mathrm{d}t $$

subject to:

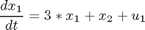
$$ \frac{dx_1}{dt} = 3*x_1+x_2 + u_1 $$

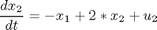
$$ \frac{dx_2}{dt} = -x_1+2*x_2 + u_2 $$

$$ x_1(0) = 4 $$

$$ x_2(0) = -4 $$

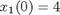
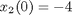
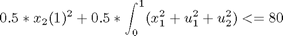
$$ 0.5*x_2(1)^2 + 0.5*\int_0^1 (x_1^2 + u_1^2 + u_2^2) <= 80 $$

Introduce a new variable to remove integral in constraint:

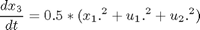
$$ \frac{dx_3}{dt} = 0.5 * (x_1.^2 + u_1.^2 + u_2.^2) $$

resulting in event constraint:

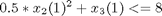
$$ 0.5*x_2(1)^2 + x_3(1) <= 8 $$

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, 0, 1, 50);
setPhase(p);

tomStates x1 x2 x3
tomControls u1 u2

% Initial guess
x0 = {icollocate({
    x1 == 4-5*t
    x2 == -4-1*t
    x3 == 50*t
    })
    collocate({
    u1 == -10+10*t
    u2 == 14-12*t})};

% Boundary constraints
cbnd = {
    initial({
    x1 == 4
    x2 == -4
    x3 == 0
    })
    final(x2)^2/2+final(x3) <= 80};

% ODEs and path constraints
ceq = collocate({
    dot(x1) == 3*x1+x2 + u1
    dot(x2) == -x1+2*x2 + u2
    dot(x3) == 1/2 * (x2.^2 + u1.^2 + u2.^2)
    });

% Objective
objective = final(x1)^2/2 + final(x3);

Solve the problem

options = struct;
options.name = 'Quadratic Constraint';
solution = ezsolve(objective, {cbnd, ceq}, x0, options);
t  = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
x3 = subs(collocate(x3),solution);
u1 = subs(collocate(u1),solution);
u2 = subs(collocate(u2),solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Quadratic Constraint           f_k      67.888740121887395000
                                       sum(|constr|)      0.000000192425266868
                              f(x_k) + sum(|constr|)     67.888740314312656000
                                              f(x_0)     50.499999999999943000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   32 ConJacEv   32 Iter   31 MinorIter  280
CPU time: 0.515625 sec. Elapsed time: 0.531000 sec.

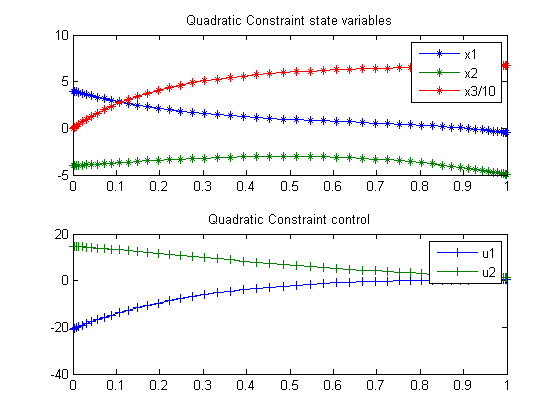
Plot result

subplot(2,1,1)
plot(t,x1,'*-',t,x2,'*-',t,x3/10,'*-');
legend('x1','x2','x3/10');
title('Quadratic Constraint state variables');

subplot(2,1,2)
plot(t,u1,'+-',t,u2,'+-');
legend('u1','u2');
title('Quadratic Constraint control');