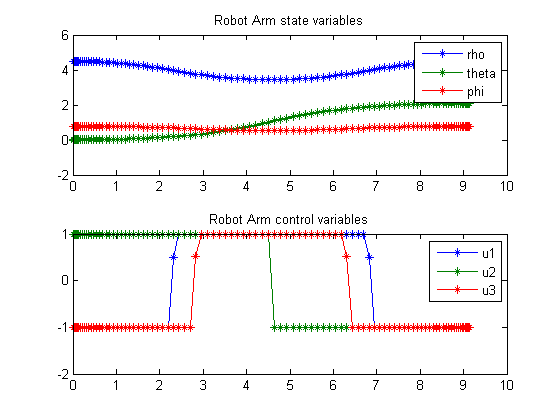
Robot Arm Movement

Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY

Contents

Problem Formulation

Find u(t) over t in [0; 1 ] to minimize

$$ J = t_f $$

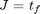
subject to:

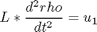
$$ L*\frac{d^{2}rho}{dt^{2}} = u_1 $$

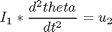
$$ I_1*\frac{d^{2}theta}{dt^{2}} = u_2 $$

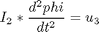
$$ I_2*\frac{d^{2}phi}{dt^{2}} = u_3 $$

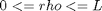
$$ 0 <= rho <= L $$

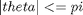
$$ |theta| <= pi $$

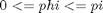
$$ 0 <= phi <= pi $$

$$ |u_{1:3}| <= 1 $$

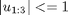
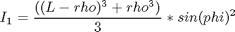
$$ I_1 = \frac{((L-rho)^3+rho^3)}{3}*sin(phi)^2 $$

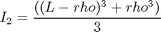
$$ I_2 = \frac{((L-rho)^3+rho^3)}{3} $$

The boundary conditions are:

$$ [rho_0 \ theta_0 \ phi_0] = [4.5 \ 0 \ \frac{pi}{4}] $$

$$ [rho_1 \ theta_1 \ phi_1] = [4.5 \ \frac{2*pi}{3} \ \frac{pi}{4}] $$

$$ L = 5 $$

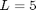
All first order derivatives are 0 at boundaries.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
toms tf

% Initial guess
tfopt = 1;
x1opt = 4.5;
x2opt = 0;
x3opt = 2*pi/3*t.^2;
x4opt = 0;
x5opt = pi/4;
x6opt = 0;
u1opt = 0;
u2opt = 0;
u3opt = 0;

for n=[20 100]

    %rho d(rho)dt theta d(theta)dt phi d(phi)dt
    p = tomPhase('p', t, 0, tf, n);
    setPhase(p);
    tomStates x1 x2 x3 x4 x5 x6
    tomControls u1 u2 u3

    % Initial guess
    x0 = {tf == tfopt
        icollocate({x1 == x1opt
        x2 == x2opt; x3 == x3opt
        x4 == x4opt; x5 == x5opt
        x6 == x6opt})
        collocate({u1 == u1opt
        u2 == u2opt; u3 == u3opt})};

    % Box constraints
    L = 5;
    cbox = {
        0.1 <= tf <= 10
        0   <= icollocate(x1) <= L
        -pi <= icollocate(x3) <= pi
        0   <= icollocate(x5) <= pi
        -1  <= collocate(u1)  <= 1
        -1  <= collocate(u2)  <= 1
        -1  <= collocate(u3)  <= 1};

    % Boundary constraints
    cbnd = {initial({x1 == 4.5; x2 == 0
        x3 == 0; x4 == 0
        x5 == pi/4; x6 == 0})
        final({x1 == 4.5; x2 == 0
        x3 == 2*pi/3
        x4 == 0
        x5 == pi/4
        x6 == 0
        })};

    I1 = ((L-x1).^3+x1.^3)./3.*sin(x5).^2;
    I2 = ((L-x1).^3+x1.^3)/3;

    % ODEs and path constraints
    ceq = collocate({dot(x1) == x2
        dot(x2) == u1/L;   dot(x3) == x4
        dot(x4) == u2./I1; dot(x5) == x6
        dot(x6) == u3./I2});

    % Objective
    objective = tf;

Solve the problem

    options = struct;
    options.name = 'Robot Arm';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

    % Optimal x, y, and speed, to use as starting guess in the next iteration
    x1opt = subs(x1, solution);
    x2opt = subs(x2, solution);
    x3opt = subs(x3, solution);
    x4opt = subs(x4, solution);
    x5opt = subs(x5, solution);
    u1opt = subs(u1, solution);
    u2opt = subs(u2, solution);
    u3opt = subs(u3, solution);
    tfopt = subs(final(t), solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Robot Arm                      f_k       9.146367586242577700
                                       sum(|constr|)      0.000001641938376501
                              f(x_k) + sum(|constr|)      9.146369228180955000
                                              f(x_0)      1.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   15 ConJacEv   15 Iter   10 MinorIter  267
CPU time: 0.093750 sec. Elapsed time: 0.093000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Robot Arm                      f_k       9.140854009735496900
                                       sum(|constr|)      0.000002639173276572
                              f(x_k) + sum(|constr|)      9.140856648908773300
                                              f(x_0)      9.146367586242577700

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    7 ConJacEv    7 Iter    4 MinorIter  723
CPU time: 1.828125 sec. Elapsed time: 1.828000 sec. 

end

t  = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x3 = subs(collocate(x3),solution);
x5 = subs(collocate(x5),solution);
u1 = subs(collocate(u1),solution);
u2 = subs(collocate(u2),solution);
u3 = subs(collocate(u3),solution);

Plot result

subplot(2,1,1)
plot(t,x1,'*-',t,x3,'*-',t,x5,'*-');
legend('rho','theta','phi');
title('Robot Arm state variables');

subplot(2,1,2)
plot(t,u1,'*-',t,u2,'*-',t,u3,'*-');
legend('u1','u2','u3');
title('Robot Arm control variables');