Satellite Control

Users Guide for dyn.Opt, Example 7a, 7b, 7c

Contents

A satellite control problem

Find T (controls) over t in [0; 100 ] to minimize

7c is free end time

7a:

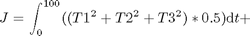
$$ J = \int_0^{100} ((T1^2+T2^2+T3^2)*0.5) \mathrm{d}t + $$

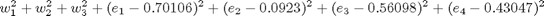
$$ w_1^2 + w_2^2 + w_3^2 + (e_1 - 0.70106)^2 + (e_2 - 0.0923)^2 + (e_3 - 0.56098)^2 + (e_4 - 0.43047)^2 $$

7b:

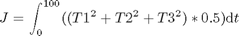
$$ J = \int_0^{100} ((T1^2+T2^2+T3^2)*0.5) \mathrm{d}t $$

7c:

$$ J = t_F $$

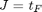
subject to:

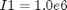
$$ I1 = 1.0e6 $$

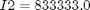
$$ I2 = 833333.0 $$

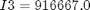
$$ I3 = 916667.0 $$

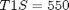
$$ T1S = 550 $$

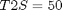
$$ T2S = 50 $$

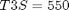
$$ T3S = 550 $$

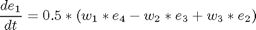
$$ \frac{de_1}{dt} = 0.5*(w_1*e_4-w_2*e_3+w_3*e_2) $$

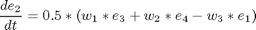
$$ \frac{de_2}{dt} = 0.5*(w_1*e_3+w_2*e_4-w_3*e_1) $$

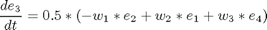
$$ \frac{de_3}{dt} = 0.5*(-w_1*e_2+w_2*e_1+w_3*e_4) $$

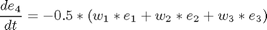
$$ \frac{de_4}{dt} = -0.5*(w_1*e_1+w_2*e_2+w_3*e_3) $$

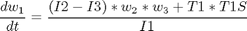
$$ \frac{dw_1}{dt} = \frac{(I2-I3)*w_2*w_3+T1*T1S}{I1} $$

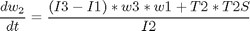
$$ \frac{dw_2}{dt} = \frac{(I3-I1)*w3*w1+T2*T2S}{I2} $$

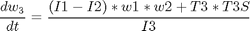
$$ \frac{dw_3}{dt} = \frac{(I1-I2)*w1*w2+T3*T3S}{I3} $$

$$ e(0) = [0 \ 0 \ 0 \ 1] $$

$$ w(0) = [0.01 \ 0.005 \ 0.001] $$

7b, 7c - x(100) = [0.70106 0.0923 0.56098 NaN 0 0 0]; 7c - free time 7c - -1 <= T <= 1

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t

% Starting guess
e1opt = 0;
e2opt = 0;
e3opt = 0;
e4opt = 0;
w1opt = 0;
w2opt = 0;
w3opt = 0;
T1opt = 0;
T2opt = 0;
T3opt = 0;

% Final times
tfs = zeros(3,1);

for i=1:3
    if i == 3
        toms tf
        runs = [10 20 101];
    else
        runs = [10 40];
    end
    if i == 2
        e1opt = 0; e2opt = 0;
        e3opt = 0; e4opt = 0;
        w1opt = 0; w2opt = 0;
        w3opt = 0; T1opt = 0;
        T2opt = 0; T3opt = 0;
    end
    for n=runs

        if i == 3
            p = tomPhase('p', t, 0, tf, n);
        else
            p = tomPhase('p', t, 0, 100, n);
        end

        setPhase(p);
        tomStates e1 e2 e3 e4 w1 w2 w3
        tomControls T1 T2 T3

        if i == 3
            x0 = {tf == 100};
        else
            x0 = {};
        end
        % Initial guess
        x0 = {x0; collocate({T1 == T1opt
            T2 == T2opt; T3 == T3opt})
            icollocate({
            e1 == e1opt; e2 == e2opt
            e3 == e3opt; e4 == e4opt
            w1 == w1opt; w2 == w2opt
            w3 == w3opt})};

        if i == 3
            cbox = {
                1 <= tf <= 1000
                -1 <= collocate(T1) <= 1
                -1 <= collocate(T2) <= 1
                -1 <= collocate(T3) <= 1};
        else
            cbox = {};
        end

        % Boundary constraints
        cbnd = initial({e1 == 0
            e2 == 0;     e3 == 0
            e4 == 1;     w1 == 0.01
            w2 == 0.005; w3 == 0.001});

Problem 7b and 7c modifications

        if i ~= 1
            cbnd = {cbnd
                final({
                e1 == 0.70106
                e2 == 0.0923
                e3 == 0.56098
                w1 == 0
                w2 == 0
                w3 == 0
                })};
        end

        % ODEs and path constraints
        I1 = 1.0e6;
        I2 = 833333.0;
        I3 = 916667.0;
        T1S = 550;
        T2S = 50;
        T3S = 550;
        ceq = collocate({
            dot(e1) == 0.5*(w1.*e4-w2.*e3+w3.*e2)
            dot(e2) == 0.5*(w1.*e3+w2.*e4-w3.*e1)
            dot(e3) == 0.5*(-w1.*e2+w2.*e1+w3.*e4)
            dot(e4) == -0.5*(w1.*e1+w2.*e2+w3.*e3)
            dot(w1) == ((I2-I3)*w2.*w3+T1*T1S)/I1
            dot(w2) == ((I3-I1)*w3.*w1+T2*T2S)/I2
            dot(w3) == ((I1-I2)*w1.*w2+T3*T3S)/I3});

        % Objective
        if i == 1
            objective = final(w1)^2 + final(w2)^2 + final(w3)^2 +...
                (final(e1) - 0.70106)^2 + (final(e2) - 0.0923)^2 + ...
                (final(e3) - 0.56098)^2 + (final(e4) - 0.43047)^2 ...
                + integrate((T1.^2+T2.^2+T3.^2)*0.5);
        elseif i == 2
            objective = integrate((T1.^2+T2.^2+T3.^2)*0.5);
        else
            objective = tf;
        end

Solve the problem

        options = struct;
        if i == 1
            options.name = 'Satellite Control 7a';
        elseif i == 2
            options.name = 'Satellite Control 7b';
        else
            options.name = 'Satellite Control 7c';
        end
        solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

        e1opt = subs(e1, solution);
        e2opt = subs(e2, solution);
        e3opt = subs(e3, solution);
        e4opt = subs(e4, solution);
        w1opt = subs(w1, solution);
        w2opt = subs(w2, solution);
        w3opt = subs(w3, solution);
        T1opt = subs(T1, solution);
        T2opt = subs(T2, solution);
        T3opt = subs(T3, solution);

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7a           f_k       0.463944669252504550
                                       sum(|constr|)      0.000000135115457319
                              f(x_k) + sum(|constr|)      0.463944804367961870
                                              f(x_0)      0.139185999999999230

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   27 ConJacEv   27 Iter   15 MinorIter  105
CPU time: 0.109375 sec. Elapsed time: 0.125000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7a           f_k       0.463944366974704090
                                       sum(|constr|)      0.000000000342698366
                              f(x_k) + sum(|constr|)      0.463944367317402460
                                              f(x_0)     -0.536077645550793400

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    3 ConJacEv    3 Iter    2 MinorIter   89
CPU time: 0.171875 sec. Elapsed time: 0.172000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7b           f_k      71.411903807059261000
                                       sum(|constr|)      0.000000066784327430
                              f(x_k) + sum(|constr|)     71.411903873843585000
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   20 ConJacEv   20 Iter   17 MinorIter  205
CPU time: 0.109375 sec. Elapsed time: 0.109000 sec. 

Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7b           f_k      71.411584008717440000
                                       sum(|constr|)      0.000000016456711387
                              f(x_k) + sum(|constr|)     71.411584025174150000
                                              f(x_0)     71.236662445283258000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    5 ConJacEv    5 Iter    3 MinorIter  350
CPU time: 0.390625 sec. Elapsed time: 0.391000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7c           f_k      99.185340224824486000
                                       sum(|constr|)      0.000000000397831665
                              f(x_k) + sum(|constr|)     99.185340225222319000
                                              f(x_0)    100.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   10 ConJacEv   10 Iter    8 MinorIter   96
CPU time: 0.078125 sec. Elapsed time: 0.078000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7c           f_k      98.945461991023606000
                                       sum(|constr|)      0.000017742910587798
                              f(x_k) + sum(|constr|)     98.945479733934192000
                                              f(x_0)    100.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    5 ConJacEv    5 Iter    4 MinorIter  155
CPU time: 0.109375 sec. Elapsed time: 0.109000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Satellite Control 7c           f_k      98.834204968061897000
                                       sum(|constr|)      0.000012503593125482
                              f(x_k) + sum(|constr|)     98.834217471655023000
                                              f(x_0)    100.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    7 ConJacEv    7 Iter    6 MinorIter  972
CPU time: 7.906250 sec. Elapsed time: 8.016000 sec. 

    end
    tfs(i) = subs(final(t),solution);
    % We only want to plot the solution from the first problem
    if i == 1
        tp  = subs(collocate(t),solution);
        e1p = subs(collocate(e1),solution);
        e2p = subs(collocate(e2),solution);
        e3p = subs(collocate(e3),solution);
        e4p = subs(collocate(e4),solution);
        w1p = subs(collocate(w1),solution);
        w2p = subs(collocate(w2),solution);
        w3p = subs(collocate(w3),solution);
        T1p = subs(collocate(T1),solution);
        T2p = subs(collocate(T2),solution);
        T3p = subs(collocate(T3),solution);
    end
end

disp(sprintf('\nFinal time for 7a = %1.4g',tfs(1)));
disp(sprintf('\nFinal time for 7b = %1.4g',tfs(2)));
disp(sprintf('\nFinal time for 7c = %1.4g',tfs(3)));

Final time for 7a = 100

Final time for 7b = 100

Final time for 7c = 98.83

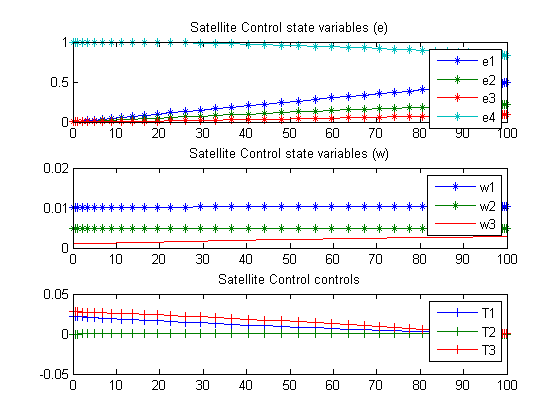
Plot result

subplot(3,1,1)
plot(tp,e1p,'*-',tp,e2p,'*-',tp,e3p,'*-',tp,e4p,'*-');
legend('e1','e2','e3','e4');
title('Satellite Control state variables (e)');

subplot(3,1,2)
plot(tp,w1p,'*-',tp,w2p,'*-',tp,w3p);
legend('w1','w2','w3');
title('Satellite Control state variables (w)');

subplot(3,1,3)
plot(tp,T1p,'+-',tp,T2p,'+-',tp,T3p,'+-');
legend('T1','T2','T3');
title('Satellite Control controls');