Space Shuttle Reentry

SOCS 6.5.0 Manual

7.4.4 Maximum Crossrange Space Shuttle Reentry Problem.

Contents

Problem Formulation

Find u over t in [0; t ] to maximize

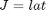
subject to:

The equations given in the code below.

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t t_f

% Scaled time
p1 = tomPhase('p1', t, 0, t_f, 30);
setPhase(p1);

tomStates alt long lat vel ggamma azi
tomControls aalpha bbeta

% Constants
tGuess = 2000;
tMax   = 4000;
tMin   = 100;
cr2d    = 180/pi;
betalim = 90;
weight  = 203000;
cm2w    = 32.174;
cea     = 20902900;
mmu      = 0.14076539e17;
rho0    = 0.002378;
href    = 23800;
cl0     = -0.20704;
cl1     = 0.029244;
cd0     = 0.07854;
cd1     = -6.1592e-3;
cd2     = 6.21408e-4;
sref    = 2690;

alt0 = 260000;
altf = 80000;

vel0 = 25600;
velf = 2500;

% Initial guess
x0 = {
    t_f == 1000
    icollocate({
    alt   == alt0-(alt0-altf)*t/t_f
    long  == -0.5*90/cr2d
    lat   == -89/cr2d
    vel   == vel0-(vel0-velf)*t/t_f
    ggamma == -1/cr2d-4/cr2d*t/t_f
    azi   == pi/2-pi*t/t_f
    })
    collocate({
    aalpha == 0
    bbeta  == 1/cr2d
    })
    };

% Boundary constraints
cbnd = {
    initial({
    alt   == alt0
    long  == -0.5*75.3153/cr2d
    lat   == 0
    vel   == 25600
    ggamma == -1/cr2d
    azi   == 90/cr2d
    aalpha == 17/cr2d
    bbeta  == -betalim/cr2d
    })
    final({
    alt   == altf
    vel   == velf
    ggamma == -5/cr2d
    })};

% Box constraints
cbox = {
    100 <= t_f <= 5000
    0             <= icollocate(alt)   <= 300000
    -0.5*90/cr2d  <= icollocate(long)  <= 0.5*90/cr2d
    -89/cr2d      <= icollocate(lat)   <= 89/cr2d
    1000          <= icollocate(vel)   <= 40000
    -89/cr2d      <= icollocate(ggamma) <= 89/cr2d
    -pi           <= icollocate(azi)   <= pi
    -89/cr2d      <= collocate(aalpha)  <= 89/cr2d
    -betalim/cr2d <= collocate(bbeta)   <= 1/cr2d
    };

mass   = weight/cm2w;
alphad = cr2d*aalpha;
radius = cea+alt;
grav   = mmu./radius.^2;

rhodns = rho0*exp(-alt/href);
dynp   = 0.5*rhodns.*vel.^2;
subl   = cl0+cl1*alphad;
subd   = cd0+cd1+cd2*alphad.*alphad;
drag   = dynp.*subd*sref;
lift   = dynp.*subl*sref;
vrelg  = vel./radius-grav./vel;

% ODEs and path constraints
ceq = collocate({
    dot(alt) == vel.*sin(ggamma)
    dot(long) == vel.*cos(ggamma).*sin(azi)./(radius.*cos(lat))
    dot(lat) == vel.*cos(ggamma).*cos(azi)./radius
    dot(vel) == -drag./mass-grav.*sin(ggamma)
    dot(ggamma) == lift.*cos(bbeta)./(mass.*vel)+cos(ggamma).*vrelg
    dot(azi) == lift.*sin(bbeta)./(mass.*vel.*cos(ggamma))+...
    vel.*cos(ggamma).*sin(azi).*sin(lat)./(radius.*cos(lat))
    });

% Objective
objective = -final(lat)*180/pi;

Solve the problem

options = struct;
options.name = 'Shuttle Reentry';
options.Prob.SOL.optPar(30) = 100000;
options.scale = 'auto';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

Problem type appears to be: lpcon
Warning: Initial guess out of bounds for the variable long_p1 
Warning: Initial guess out of bounds for the variable lat_p1 
Auto-scaling
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2011-02-05
=====================================================================================
Problem: ---  1: Shuttle Reentry                f_k     -15.142919504969253000
                                       sum(|constr|)      0.000000003266941604
                              f(x_k) + sum(|constr|)    -15.142919501702311000
                                              f(x_0)     -0.000000000000909495

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv 6998 ConJacEv 6996 Iter  792 MinorIter 17775
CPU time: 118.937500 sec. Elapsed time: 64.438000 sec. 

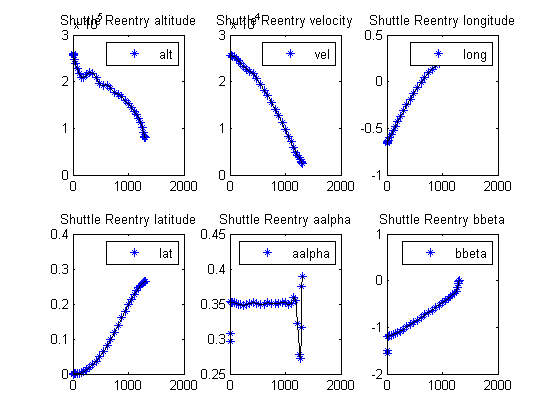
Plot result

subplot(2,3,1)
ezplot(alt)
legend('alt');
title('Shuttle Reentry altitude');

subplot(2,3,2)
ezplot(vel)
legend('vel');
title('Shuttle Reentry velocity');

subplot(2,3,3)
ezplot(long)
legend('long');
title('Shuttle Reentry longitude');

subplot(2,3,4)
ezplot(lat)
legend('lat');
title('Shuttle Reentry latitude');

subplot(2,3,5)
ezplot(aalpha)
legend('aalpha');
title('Shuttle Reentry aalpha');

subplot(2,3,6)
ezplot(bbeta)
legend('bbeta');
title('Shuttle Reentry bbeta');