Simple Bang Bang Problem

Function Space Complementarity Methods for Optimal Control Problems, Dissertation, Martin Weiser

Contents

Problem Description

Find u over t in [-0.5; 0.5 ] to minimize:

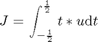
$$ J = \int_{-\frac{1}{2}}^{\frac{1}{2}} t*u \mathrm{d}t $$

subject to:

$$ |u| <= 1 $$

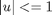
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, -0.5, 1, 20);
setPhase(p);
tomStates x
tomControls u

% Initial guess
x0 = {collocate(u == 1-2*(t+0.5))
    icollocate(x == 1-2*(t+0.5))};

% Box constraints
cbox = {-1 <= icollocate(x) <= 1
    -1 <= collocate(u)  <= 1};

% ODEs and path constraints
ceq = collocate(dot(x) == 0);

% Objective
objective = integrate(t.*u);

Solve the problem

options = struct;
options.name = 'Simple Bang Bang Problem';
solution = ezsolve(objective, {cbox, ceq}, x0, options);
t = subs(collocate(t),solution);
u = subs(collocate(u),solution);

Problem type appears to be: lp
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Simple Bang Bang Problem       f_k      -0.250490325030179710
                                       sum(|constr|)      0.000000000000810402
                              f(x_k) + sum(|constr|)     -0.250490325029369300
                                              f(x_0)      0.000000000000000000

Solver: CPLEX.  EXIT=0.  INFORM=1.
CPLEX Dual Simplex LP solver
Optimal solution found

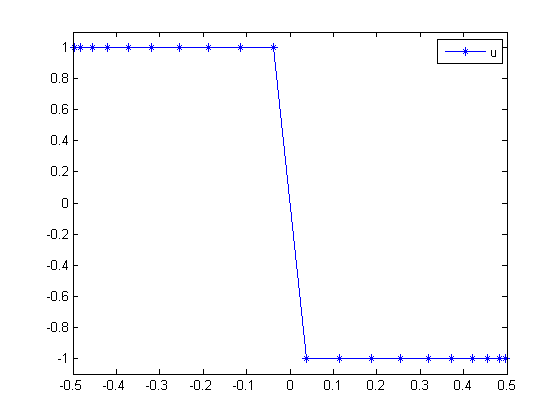
Plot result

figure(1);
plot(t,u,'*-');
legend('u');
ylim([-1.1,1.1]);