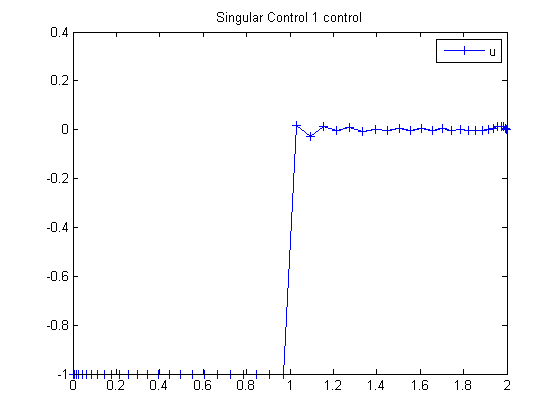
Singular Control 1

ITERATIVE DYNAMIC PROGRAMMING, REIN LUUS

10.2.1 Example 1

CHAPMAN & HALL/CRC Monographs and Surveys in Pure and Applied Mathematics

Contents

Problem Formulation

Find u over t in [0; 2 ] to minimize

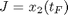
$$ J = x_2(t_F) $$

subject to:

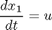
$$ \frac{dx_1}{dt} = u $$

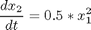
$$ \frac{dx_2}{dt} = 0.5*x_1^2 $$

The initial condition are:

$$ x(0) = [1 \ 0] $$

$$ -1 <= u <= 1 $$

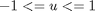
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

Problem setup

toms t
p = tomPhase('p', t, 0, 2, 50);
setPhase(p);

tomStates x1 x2
tomControls u

% Initial guess
x0 = {icollocate({x1 == 1; x2 == 0})
    collocate(u == 0)};

% Box constraints
cbox = {-1 <= collocate(u) <= 1};

% Boundary constraints
cbnd = initial({x1 == 1; x2 == 0});

% ODEs and path constraints
ceq = collocate({dot(x1) == u
    dot(x2) == 0.5*x1.^2});

% Objective
objective = final(x2);

Solve the problem

options = struct;
options.name = 'Singular Control 1';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
t = subs(collocate(t),solution);
u = subs(collocate(u),solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Singular Control 1             f_k       0.166665695130345570
                                       sum(|constr|)      0.000000330655498898
                              f(x_k) + sum(|constr|)      0.166666025785844470
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   41 ConJacEv   41 Iter   39 MinorIter  191
CPU time: 0.187500 sec. Elapsed time: 0.188000 sec.

Plot result

figure(1)
plot(t,u,'+-');
legend('u');
title('Singular Control 1 control');