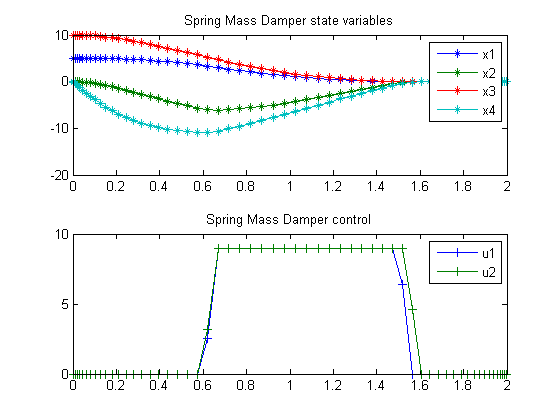
Spring Mass Damper (2 Degree Freedom)
The Direct Approach of General Dynamic Optimal Control: Application on General Software
Tawiwat Veeraklaew, Ph.D. and Settapong Malisuwan, Ph.D. Chulachomklao Royal Military Academy Nakhon-Nayok, Thailand
Contents
Problem Formulation
Find u over t in [0; 2 ] to minimize
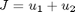
subject to:
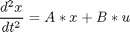
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
toms t p = tomPhase('p', t, 0, 2, 60); setPhase(p); tomStates x1 x2 x3 x4 tomControls u1 u2 x = [x1;x2;x3;x4]; u = [u1;u2]; m1 = 1.0; m2 = 1.0; c1 = 1.0; c3 = 1.0; c2 = 2.0; k1 = 3.0; k2 = 3.0; k3 = 3.0; B = [0 0; 1/m1 0; 0 0; 0 1/m2]; A = [0 1 0 0;... 1/m1*[-(k1+k2) -(c1+c2) k2 c2];... 0 0 0 1;... 1/m2*[ k2 c2 -(k2+k3) -(c2+c3)]]; x0i = [5; 0; 10; 0]; xfi = [0; 0; 0; 0]; % Box constraints cbox = {0 <= collocate(u) <= 9}; % Boundary constraints cbnd = {initial(x == x0i) final(x == xfi)}; % ODEs and path constraints ceq = collocate(dot(x) == A*x+B*u); % Objective objective = integrate(u1+u2);
Solve the problem
options = struct;
options.name = 'Spring Mass Damper';
solution = ezsolve(objective, {cbox, cbnd, ceq}, [], options);
t = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
x3 = subs(collocate(x3),solution);
x4 = subs(collocate(x4),solution);
u1 = subs(collocate(u1),solution);
u2 = subs(collocate(u2),solution);
Problem type appears to be: lp
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Spring Mass Damper f_k 16.485256203068737000
sum(|constr|) 0.000000008199340966
f(x_k) + sum(|constr|) 16.485256211268076000
f(x_0) 0.000000000000000000
Solver: CPLEX. EXIT=0. INFORM=1.
CPLEX Dual Simplex LP solver
Optimal solution found
FuncEv 243 Iter 243
CPU time: 0.078125 sec. Elapsed time: 0.078000 sec.
Plot result
subplot(2,1,1) plot(t,x1,'*-',t,x2,'*-',t,x3,'*-',t,x4,'*-'); legend('x1','x2','x3','x4'); title('Spring Mass Damper state variables'); subplot(2,1,2) plot(t,u1,'+-',t,u2,'+-'); legend('u1','u2'); title('Spring Mass Damper control');