Tubular Reactor

Global Optimization of Chemical Processes using Stochastic Algorithms 1996, Julio R. Banga, Warren D. Seider

Case Study V: Global optimization of a bifunctional catalyst blend in a tubular reactor

Contents

Problem Description

Luus et al and Luus and Bojkov consider the optimization of a tubular reactor in which methylcyclopentane is converted into benzene. The blend of two catalysts, for hydrogenation and isomerization is described by the mass fraction u of the hydrogenation catalyst. The optimal control problem is to find the catalyst blend along the length of the reactor defined using a characteristic reaction time t in the interval 0 <= t <= tf where tf = 2000 gh/mol corresponding to the reactor exit such that the benzene concentration at the exit of the reactor is maximized.

Find u(t) to maximize:

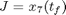
$$ J = x_7(t_f) $$

Subject to:

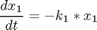
$$ \frac{dx_1}{dt} = -k_1*x_1 $$

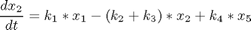
$$ \frac{dx_2}{dt} = k_1*x_1-(k_2+k_3)*x_2+k_4*x_5 $$

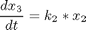
$$ \frac{dx_3}{dt} = k_2*x_2 $$

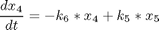
$$ \frac{dx_4}{dt} = -k_6*x_4+k_5*x_5 $$

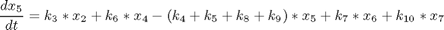
$$ \frac{dx_5}{dt} = k_3*x_2+k_6*x_4-(k_4+k_5+k_8+k_9)*x_5+k_7*x_6+k_{10}*x_7 $$

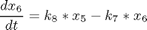
$$ \frac{dx_6}{dt} = k_8*x_5-k_7*x_6 $$

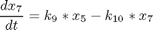
$$ \frac{dx_7}{dt} = k_9*x_5-k_{10}*x_7 $$

where xi, i = 1,..,7 are the mole fractions of the chemical species (i = 1 for methylcyclopentane, i = 7 for benzene), the rate constants are functions of the catalyst blend u(t):

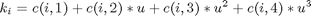
$$ k_i = c(i,1)+c(i,2)*u+c(i,3)*u^2+c(i,4)*u^3 $$

and the coefficients cij are given by Luus et al. The upper and lower bounds on the mass fraction of the hydrogenation catalyst are.

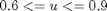
$$ 0.6 <= u <= 0.9 $$

The initial vector of mole fractions is:

$$ x(t_0) = [1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0]' $$

% Copyright (c) 2007-2008 by Tomlab Optimization Inc.

% Data
c = [0.2918487e-2, -0.8045787e-2, 0.6749947e-2,  -0.1416647e-2;...
    0.9509977e1,   -0.3500994e2,  0.4283329e2,   -0.1733333e2; ...
    0.2682093e2,   -0.9556079e2,  0.1130398e3,   -0.4429997e2; ...
    0.2087241e3,   -0.7198052e3,  0.8277466e3,   -0.3166655e3; ...
    0.1350005e1,   -0.6850027e1,  0.1216671e2,   -0.6666689e1; ...
    0.1921995e-1,  -0.7945320e-1, 0.1105666,     -0.5033333e-1;...
    0.1323596,     -0.4696255,    0.5539323,     -0.2166664;   ...
    0.7339981e1,   -0.2527328e2,  0.2993329e2,   -0.1199999e2; ...
    -0.3950534,     0.1679353e1,  -0.1777829e1,  0.4974987;    ...
    -0.2504665e-4,  0.1005854e-1, -0.1986696e-1, 0.9833470e-2]';

% Independent variable
toms t

% Initial guess
x1opt = 1; x2opt = 0;
x3opt = 0; x4opt = 0;
x5opt = 0; x6opt = 0;
x7opt = 0; uopt = 0.9;

% Loop over number of collocation points
for n=[10 80]

Problem setup

    p = tomPhase('p', t, 0, 2000, n);
    setPhase(p);

    tomStates x1 x2 x3 x4 x5 x6 x7
    tomControls u

    % Collocate initial guess
    x0 = {icollocate({x1 == x1opt; x2 == x2opt
        x3 == x3opt; x4 == x4opt; x5 == x5opt
        x6 == x6opt; x7 == x7opt})
        collocate(u == uopt)};

    % Box constraints
    cbox = {icollocate({
        0 <= x1 <= 1; 0 <= x2 <= 1
        0 <= x3 <= 1; 0 <= x4 <= 1
        0 <= x5 <= 1; 0 <= x6 <= 1
        0 <= x7 <= 1})
        0.6 <= collocate(u) <= 0.9};

    % Boundary constraints
    cbnd = initial({x1 == 1; x2 == 0
        x3 == 0; x4 == 0; x5 == 0
        x6 == 0; x7 == 0});

    % ODEs and path constraints
    uvec = [1, u, u.^2, u.^3];
    k    = (c'*uvec')';
    ceq = collocate({
        dot(x1) == -k(1)*x1
        dot(x2) ==  k(1)*x1-(k(2)+k(3))*x2+k(4)*x5
        dot(x3) ==  k(2)*x2
        dot(x4) == -k(6)*x4+k(5)*x5
        dot(x5) ==  k(3)*x2+k(6)*x4-(k(4)+k(5)+k(8)+k(9))*x5+...
        k(7)*x6+k(10).*x7
        dot(x6) == k(8)*x5-k(7)*x6
        dot(x7) == k(9)*x5-k(10)*x7});

    % Objective
    objective = -final(x7);
    options = struct;
    options.name = 'Tubular Reactor';
    options.d2c = false;
    Prob = sym2prob('con',objective,{cbox, cbnd, ceq}, x0, options);
    Prob.xInit = 35; % Use 35 random starting points.
    Prob.GO.localSolver = 'snopt';
    if n<=10
        Result = tomRun('multiMin', Prob, 1);
    else
        Result = tomRun('snopt', Prob, 1);
    end
    solution = getSolution(Result);

    % Store optimum for use in initial guess
    x1opt = subs(x1,solution);
    x2opt = subs(x2,solution);
    x3opt = subs(x3,solution);
    x4opt = subs(x4,solution);
    x5opt = subs(x5,solution);
    x6opt = subs(x6,solution);
    x7opt = subs(x7,solution);
    uopt  = subs(u,solution);

===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Tubular Reactor                f_k      -0.010093482963145356
                                       sum(|constr|)      0.000000004467202512
                              f(x_k) + sum(|constr|)     -0.010093478495942844
                                              f(x_0)     -1.010438967758588500

Solver: multiMin with local solver snopt.  EXIT=0.  INFORM=1.
Find local optima using multistart local search
Did 35 local tries. Found 31 local minima

FuncEv   31 GradEv   29 ConstrEv   29 ConJacEv   29 Iter   19 MinorIter  204
CPU time: 5.312500 sec. Elapsed time: 5.359000 sec. 

===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Tubular Reactor                f_k      -0.010082374590765433
                                       sum(|constr|)      0.000000000045366255
                              f(x_k) + sum(|constr|)     -0.010082374545399177
                                              f(x_0)     -0.010093482963145358

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv   51 GradEv   49 ConstrEv   49 ConJacEv   49 Iter   34 MinorIter  490
CPU time: 4.953125 sec. Elapsed time: 5.062000 sec. 

end

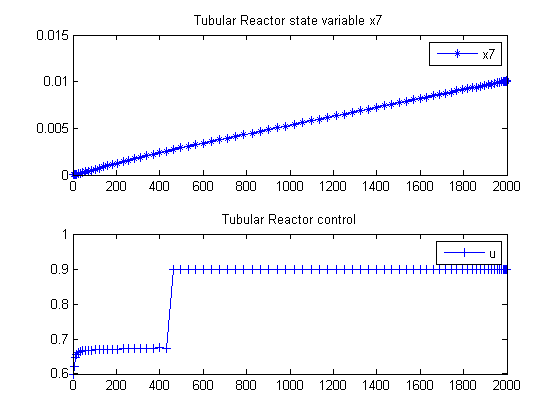
Plot result

t  = collocate(t);
x7 = collocate(x7opt);
u  = collocate(uopt);

subplot(2,1,1)
plot(t,x7,'*-');
legend('x7');
title('Tubular Reactor state variable x7');

subplot(2,1,2)
plot(t,u,'+-');
legend('u');
title('Tubular Reactor control');