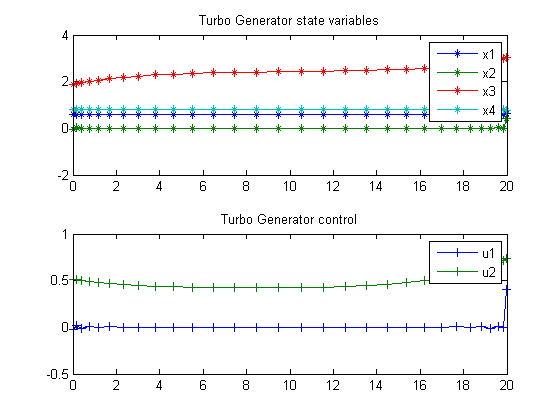
Turbo Generator
OCCAL - A Mixed symbolic-numeric Optimal Control CALcluator
Section 4 Example 1
Contents
Problem Formulation
Find u over t in [0; t ] to minimize
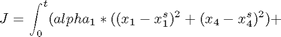
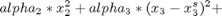
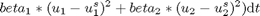
subject to:
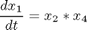

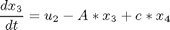
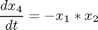
The initial condition are:
![$$ x(0) = [x_1^{s} \ x_2^{s} \ x_3^{s} \ x_4^{s}] $$](xturboGenerator_eq03842.png)
![$$ x_{1:4}^{s} = [0.60295 \ 0.0 \ 1.87243 \ 0.79778] $$](xturboGenerator_eq90562.png)
![$$ alpha = [2.5 \ 1.0 \ 0.1] $$](xturboGenerator_eq55631.png)
![$$ beta = [1.0 \ 1.0] $$](xturboGenerator_eq46841.png)
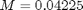
![$$ s_{4:5} = [0.0 \ 0.0] $$](xturboGenerator_eq22901.png)
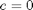
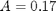
![$$ u_{1:2}^{s} = [0.80 \ 0.73962] $$](xturboGenerator_eq29049.png)
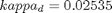
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.
Problem setup
toms t p = tomPhase('p', t, 0, 20, 30); setPhase(p); tomStates x1 x2 x3 x4 tomControls u1 u2 % Initial guess x0i = [0.60295;0;1.87243;0.79778]; x0 = {icollocate({x1 == x0i(1); x2 == x0i(2) x3 == x0i(3); x4 == x0i(4)}) collocate({u1 == 0; u2 == 0})}; % Boundary constraints cbnd = initial({x1 == x0i(1); x2 == x0i(2) x3 == x0i(3); x4 == x0i(4)}); % ODEs and path constraints u1s = 0.80; u2s = 0.73962; A = 0.17; c = 0; s4 = 0; s5 = 0; M = 0.04225; alpha1 = 2.5; alpha2 = 1.0; alpha3 = 0.1; beta1 = 1.0; beta2 = 1.0; kappa_d = 0.02535; ceq = collocate({dot(x1) == x2.*x4 dot(x2) == 1/M.*(u1-s4*x1.*x4-s5*x1.*x3-kappa_d*x2) dot(x3) == u2-A*x3+c*x4; dot(x4) == -x1.*x2}); % Objective objective = integrate(alpha1*( (x1-x0i(1)).^2 + ... (x4-x0i(4)).^2) + alpha2*x2.^2 + alpha3*(x3-x0i(3)).^2 + ... beta1*(u1-u1s).^2 + beta2*(u2-u2s).^2);
Solve the problem
options = struct;
options.name = 'Turbo Generator';
solution = ezsolve(objective, {cbnd, ceq}, x0, options);
t = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
x3 = subs(collocate(x3),solution);
x4 = subs(collocate(x4),solution);
u1 = subs(collocate(u1),solution);
u2 = subs(collocate(u2),solution);
Problem type appears to be: qpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2010-02-05
=====================================================================================
Problem: --- 1: Turbo Generator f_k 15.019841547670879000
sum(|constr|) 0.000000000046656360
f(x_k) + sum(|constr|) 15.019841547717535000
f(x_0) -57.012069754799995000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 35 ConJacEv 35 Iter 23 MinorIter 142
CPU time: 0.125000 sec. Elapsed time: 0.125000 sec.
Plot result
subplot(2,1,1) plot(t,x1,'*-',t,x2,'*-',t,x3,'*-',t,x4,'*-'); legend('x1','x2','x3','x4'); title('Turbo Generator state variables'); subplot(2,1,2) plot(t,u1,'+-',t,u2,'+-'); legend('u1','u2'); title('Turbo Generator control');