Zermelos problem (version 2)

Contents

Problem description

Time-optimal crossing by boat of a river with a position dependent current stream.

Applied Optimal Control, Bryson & Ho, 1975. Example 1 on page 77.

Programmers: Gerard Van Willigenburg (Wageningen University) Willem De Koning (retired from Delft University of Technology)

% Copyright (c) 2009-2009 by Tomlab Optimization Inc.

Problem setup

% Array with consecutive number of collocation points
narr = [20 40];

toms t tf % Free final time

for n=narr

    p = tomPhase('p', t, 0, tf, n);
    setPhase(p)

    tomStates x1 x2
    tomControls u1

    % Initial & terminal states
    xi = [0;  0];
    xf = [31; 0];

    % Initial guess
    if n==narr(1)
        x0 = {tf == 2; icollocate({x1 == xi(1); x2 == xi(2)})
            collocate({u1 == 0})};
    else
        x0 = {tf == tfopt; icollocate({x1 == xopt1; x2 == xopt2})
            collocate({u1 == uopt1})};
    end

    % Box constraints
    cbox = {1 <= tf <= 10};

    % Boundary constraints
    cbnd = {initial({x1 == xi(1); x2 == xi(2)});
        final({x1 == xf(1); x2 == xf(2)})};

    % ODEs and path constraints
    v = 9;
    % No water motion in x1 direction
    dx1 = v*cos(u1);
    % Water motion in x2 direction: 5*sin(pi*x1/31)
    dx2 = v*sin(u1)+5*sin(pi*x1/31);

    ceq = collocate({
        dot(x1) == dx1
        dot(x2) == dx2});

    % Objective
    objective = tf;

Solve the problem

    options = struct;
    options.name = 'Ferry trajectory optimization';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

    tfopt = subs(tf,solution);
    xopt1 = subs(x1,solution);
    xopt2 = subs(x2,solution);
    uopt1 = subs(u1,solution);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Ferry trajectory optimization  f_k       3.681324200251761000
                                       sum(|constr|)      0.000024237038659655
                              f(x_k) + sum(|constr|)      3.681348437290420600
                                              f(x_0)      2.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   91 ConJacEv   91 Iter   54 MinorIter  110
CPU time: 0.156250 sec. Elapsed time: 0.172000 sec. 

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Ferry trajectory optimization  f_k       3.681324335382778000
                                       sum(|constr|)      0.000002528802798087
                              f(x_k) + sum(|constr|)      3.681326864185576300
                                              f(x_0)      3.681324200251761000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   40 ConJacEv   40 Iter   32 MinorIter  114
CPU time: 0.171875 sec. Elapsed time: 0.172000 sec. 

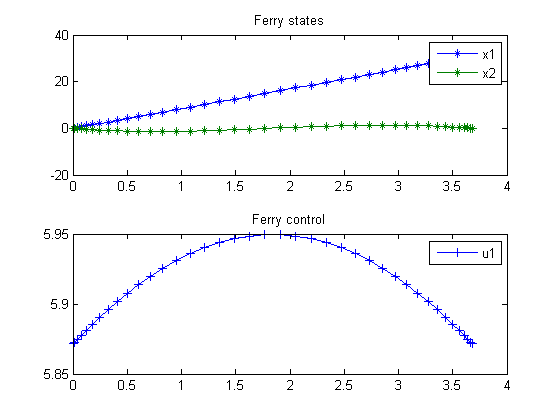
end

% Get solution
t  = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
u1 = subs(collocate(u1),solution);

%Bound u1 to [0,2pi]
u1 = rem(u1,2*pi); u1 = (u1<0)*2*pi+u1;

% Plot final solution
figure(1)
subplot(2,1,1)
plot(t,x1,'*-',t,x2,'*-');
legend('x1','x2');
title('Ferry states');

subplot(2,1,2)
plot(t,u1,'+-');
legend('u1');
title('Ferry control');